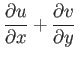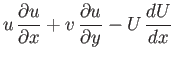Next: Boundary Layer Separation
Up: Incompressible Boundary Layers
Previous: Wake Downstream of a
Consider a boundary layer that forms on the surface of a rigid stationary obstacle of arbitrary shape (but infinite length and
uniform cross-section) placed in a steady, uniform, transverse, high Reynolds
number flow. Let  represent arc length along the surface, measured (in the direction of the external flow) from the stagnation point that forms at the front of the obstacle. (See Figure 8.11.) Moreover, let
represent arc length along the surface, measured (in the direction of the external flow) from the stagnation point that forms at the front of the obstacle. (See Figure 8.11.) Moreover, let  represent distance across the boundary layer, measured normal to the surface. Suppose that the boundary layer is
sufficiently thin that it is well approximated as a plane slab in the immediate vicinity of a general point on the
surface. In this case, writing the velocity field within the layer in the form
represent distance across the boundary layer, measured normal to the surface. Suppose that the boundary layer is
sufficiently thin that it is well approximated as a plane slab in the immediate vicinity of a general point on the
surface. In this case, writing the velocity field within the layer in the form
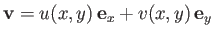 ,
it is reasonable to model this flow using the slab boundary layer equations [see Equations (8.28) and (8.29)]
,
it is reasonable to model this flow using the slab boundary layer equations [see Equations (8.28) and (8.29)]
subject to the standard boundary conditions
Here, 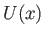 is the external tangential fluid velocity at the edge of the layer. Integrating (8.111) across the layer,
making use of the boundary conditions (8.113), leads to
is the external tangential fluid velocity at the edge of the layer. Integrating (8.111) across the layer,
making use of the boundary conditions (8.113), leads to
Here, we have integrated the final term on the right-hand side by parts, making use of Equations (8.110), (8.112), and (8.113).
Let us define the displacement thickness of the layer [see Equation (8.70)]
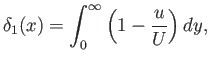 |
(8.115) |
as well as the so-called momentum thickness
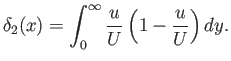 |
(8.116) |
It follows from Equation (8.114) that
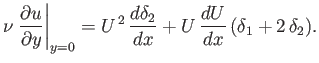 |
(8.117) |
This important result is known as the von Kármán momentum integral, and is fundamental to
many of the approximation methods commonly employed to calculate boundary layer thicknesses on the surfaces of general obstacles
placed in high Reynolds number flows. (See Section 8.10.)



Next: Boundary Layer Separation
Up: Incompressible Boundary Layers
Previous: Wake Downstream of a
Richard Fitzpatrick
2016-01-22