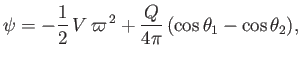where

and that the streamline, other than
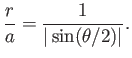
The flow pattern (7.161) can be reinterpreted as that which results when a blunt obstacle lying to the
right of the previously specified streamline is placed in a uniform stream of velocity
![]() .
Show that the obstacle in question has the asymptotic (i.e., as
.
Show that the obstacle in question has the asymptotic (i.e., as
![]() ) thickness
) thickness ![]() .
Demonstrate that the pressure distribution over the surface of the obstacle is
.
Demonstrate that the pressure distribution over the surface of the obstacle is
![$\displaystyle p = p_0 + \rho\,V^{\,2}\,\sin^2(\theta/2)\left[\frac{3}{2}\,\sin^2(\theta/2)-1\right],
$](img2821.png)
where
where
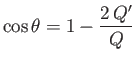
divides the streamlines issuing from
where
and
and also passes through the points
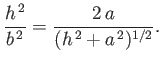
The flow pattern (7.162) can be reinterpreted as that which results when an axisymmetric solid body of oval cross-section
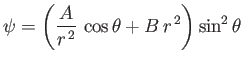
is a possible stream function for an axisymmetric, incompressible, irrotational flow pattern, and find the corresponding velocity potential. (Milne-Thompson 2011.)
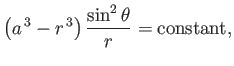
where
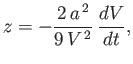
the center of the sphere being instantaneously at the origin. (Milne-Thompson 2011.)
where
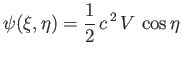
can be interpreted as that of incompressible irrotational flow, with mean speed