


Next: Convective Time Derivative
Up: Mathematical Models of Fluid
Previous: Conservation Laws
Mass Conservation
Let
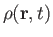 and
and
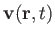 be the mass density and velocity of a given fluid at point
be the mass density and velocity of a given fluid at point  and time
and time 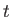 . Consider a
fixed volume
. Consider a
fixed volume  , surrounded by a surface
, surrounded by a surface  . The net mass contained within
. The net mass contained within  is
is
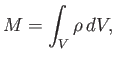 |
(1.32) |
where 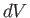 is an element of
is an element of  .
Furthermore, the mass flux across
.
Furthermore, the mass flux across  , and out of
, and out of  , is [see Equation (1.29)]
, is [see Equation (1.29)]
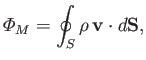 |
(1.33) |
where 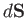 is an outward directed element of
is an outward directed element of  . Mass conservation requires
that the rate of increase of the mass contained within
. Mass conservation requires
that the rate of increase of the mass contained within  ,
plus the net mass flux out of
,
plus the net mass flux out of  , should equal zero: that is,
, should equal zero: that is,
 |
(1.34) |
[cf., Equation (1.31)].
Here, we are assuming that there is no mass generation (or destruction) within  (because individual molecules
are effectively indestructible).
It follows that
(because individual molecules
are effectively indestructible).
It follows that
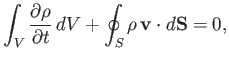 |
(1.35) |
because  is non-time-varying. Making use of the divergence theorem (see Section A.20),
the previous equation becomes
is non-time-varying. Making use of the divergence theorem (see Section A.20),
the previous equation becomes
![$\displaystyle \int_V\left[\frac{\partial \rho}{\partial t} + \nabla\cdot(\rho\,{\bf v})\right]dV = 0.$](img256.png) |
(1.36) |
However, this result is true irrespective of the size, shape, or location of volume  , which is only possible if
, which is only possible if
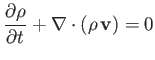 |
(1.37) |
throughout the fluid. The previous expression is known as the equation of fluid continuity, and is
a direct consequence of mass conservation.



Next: Convective Time Derivative
Up: Mathematical Models of Fluid
Previous: Conservation Laws
Richard Fitzpatrick
2016-01-22
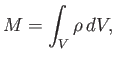
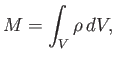
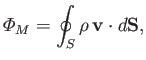

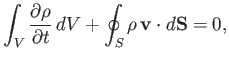
![$\displaystyle \int_V\left[\frac{\partial \rho}{\partial t} + \nabla\cdot(\rho\,{\bf v})\right]dV = 0.$](img256.png)