


Next: Normalization scheme
Up: Particle-in-cell codes
Previous: Particle-in-cell codes
Consider an unmagnetized, uniform, 1-dimensional plasma consisting of  electrons and
electrons and  unit-charged
ions.
Now, ions are much more massive than electrons.
Hence, on short time-scales, we can treat the ions as a static
neutralizing background, and only consider the motion of the electrons. Let
unit-charged
ions.
Now, ions are much more massive than electrons.
Hence, on short time-scales, we can treat the ions as a static
neutralizing background, and only consider the motion of the electrons. Let 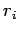 be the
be the
 -coordinate of the
-coordinate of the 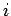 th electron. The equations of motion of the
th electron. The equations of motion of the
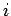 th electron are written:
th electron are written:
where  is the magnitude of the electron charge,
is the magnitude of the electron charge, 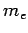 the electron mass, and
the electron mass, and 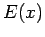 the
the  -component
of the electric field-strength at position
-component
of the electric field-strength at position  . Now, the electric field-strength can be
expressed in terms of an electric
potential:
. Now, the electric field-strength can be
expressed in terms of an electric
potential:
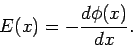 |
(291) |
Furthermore, from the Poisson-Maxwell equation, we have
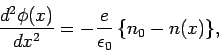 |
(292) |
where 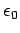 is the permittivity of free-space,
is the permittivity of free-space, 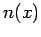 the electron number
density (i.e.,
the electron number
density (i.e., 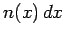 is the number of electrons in the interval
is the number of electrons in the interval  to
to 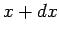 ),
and
),
and 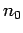 the uniform ion number density. Of course, the average value of
the uniform ion number density. Of course, the average value of 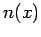 is
equal to
is
equal to 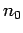 , since there are equal numbers of ions and electrons.
, since there are equal numbers of ions and electrons.
Let us consider an initial electron distribution function consisting of two counter-propagating
Maxwellian beams of mean speed 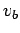 and thermal spread
and thermal spread 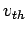 : i.e.,
: i.e.,
 |
(293) |
Here,
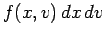 is the number of electrons between
is the number of electrons between  and
and 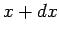 with velocities
in the range
with velocities
in the range 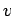 to
to 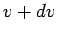 . Of course,
. Of course,
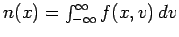 .
The beam temperature
.
The beam temperature 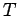 is related to the thermal velocity via
is related to the thermal velocity via
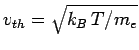 ,
where
,
where 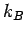 is the Boltzmann constant. It is well-known that if
is the Boltzmann constant. It is well-known that if 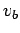 is significantly
larger than
is significantly
larger than 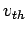 then the above distribution is unstable to a plasma instability
called the two-stream instability.38 Let us investigate this instability numerically.
then the above distribution is unstable to a plasma instability
called the two-stream instability.38 Let us investigate this instability numerically.



Next: Normalization scheme
Up: Particle-in-cell codes
Previous: Particle-in-cell codes
Richard Fitzpatrick
2006-03-29
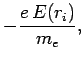
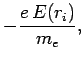
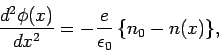
![]() and thermal spread
and thermal spread ![]() : i.e.,
: i.e.,

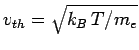 ,
where
,
where