


Next: 3-d problems
Up: Poisson's equation
Previous: An example solution of
Let us perform an example 2-d electrostatic calculation. Consider a charged wire
running parallel to the axis of a uniform, hollow, rectangular, conducting channel.
Suppose that the vertices of the channel lie at 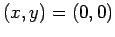 ,
, 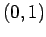 ,
,  , and
, and 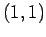 .
Suppose, further, that the wire carries a uniform charge per unit length of magnitude unity.
The electric potential
.
Suppose, further, that the wire carries a uniform charge per unit length of magnitude unity.
The electric potential 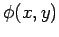 inside the channel satisfies [see Eq. (110)]
inside the channel satisfies [see Eq. (110)]
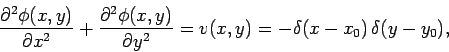 |
(185) |
where 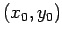 are the coordinates of the wire.
Here, we have conveniently normalized our units such that the factor
are the coordinates of the wire.
Here, we have conveniently normalized our units such that the factor 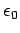 is absorbed into the normalization.
Assuming that the box is grounded, the potential is
subject to the Dirichlet boundary conditions
is absorbed into the normalization.
Assuming that the box is grounded, the potential is
subject to the Dirichlet boundary conditions 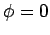 at
at 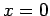 ,
, 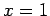 ,
, 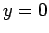 , and
, and
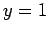 . We require the solution in the region
. We require the solution in the region  and
and
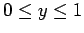 .
.
Figure 67:
Contour plot of the electric potential generated by
a charged wire placed at the center of a grounded
rectangular channel. The wire is located at
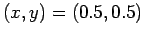 , whereas the
channel walls are at
, whereas the
channel walls are at 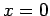 ,
, 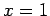 ,
, 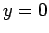 , and
, and 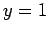 .
Calculation performed with
.
Calculation performed with 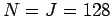 .
.
 |
Note that when discretizing Eq. (185) the right-hand side becomes
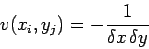 |
(186) |
on the grid-point closest to the wire, with
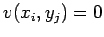 on the remaining grid-points.
Here,
on the remaining grid-points.
Here, 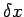 and
and 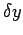 are the grid spacings in the
are the grid spacings in the  - and
- and
 - directions, respectively.
- directions, respectively.
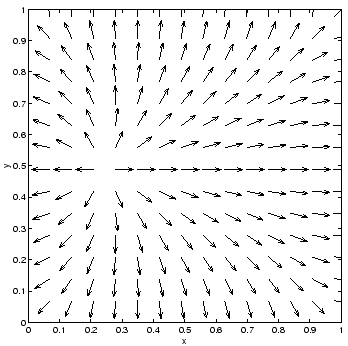
Figure 68:
Vector plot showing the direction of the electric field generated by a charged wire placed at the center of a grounded
rectangular channel. The wire is located at
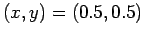 , whereas the
channel walls are at
, whereas the
channel walls are at 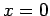 ,
, 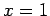 ,
, 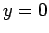 , and
, and 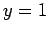 . Calculation performed with
. Calculation performed with 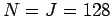 .
.
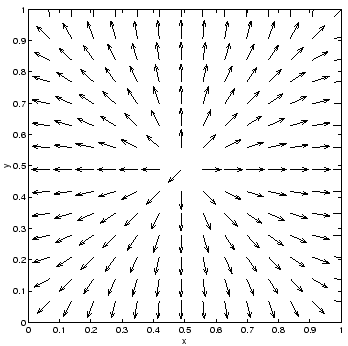 |
Figures 67 and 68 show the electric potential 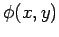 and electric
field
and electric
field
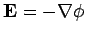 generated by a wire placed at the center of the
channel: i.e.,
generated by a wire placed at the center of the
channel: i.e.,
 . The calculation was performed with the
previously listed 2-d Poisson solver using
. The calculation was performed with the
previously listed 2-d Poisson solver using
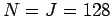 .
.
Figure 69:
Contour plot of the electric potential generated by
a charged wire offset from the center of a grounded
rectangular channel. The wire is located at
 , whereas the
channel walls are at
, whereas the
channel walls are at 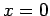 ,
, 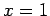 ,
, 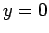 , and
, and 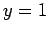 . Calculation performed with
. Calculation performed with 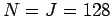 .
.
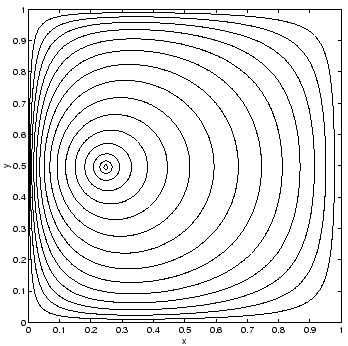 |
Figures 69 and 70 show the electric potential 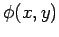 and electric
field
and electric
field
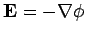 generated by a wire offset from the center of the
channel: i.e.,
generated by a wire offset from the center of the
channel: i.e.,
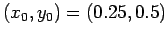 . The calculation was performed with the
previously listed 2-d Poisson solver using
. The calculation was performed with the
previously listed 2-d Poisson solver using
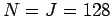 .
.
Figure 70:
Vector plot showing the direction of the electric field generated by a charged wire
offset from the center of a grounded
rectangular channel. The wire is located at
 , whereas the
channel walls are at
, whereas the
channel walls are at 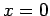 ,
, 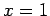 ,
, 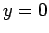 , and
, and 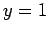 . Calculation performed with
. Calculation performed with 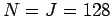 .
.
 |



Next: 3-d problems
Up: Poisson's equation
Previous: An example solution of
Richard Fitzpatrick
2006-03-29
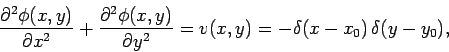


![]() and electric
field
and electric
field
![]() generated by a wire placed at the center of the
channel: i.e.,
generated by a wire placed at the center of the
channel: i.e.,
![]() . The calculation was performed with the
previously listed 2-d Poisson solver using
. The calculation was performed with the
previously listed 2-d Poisson solver using
![]() .
.

![]() and electric
field
and electric
field
![]() generated by a wire offset from the center of the
channel: i.e.,
generated by a wire offset from the center of the
channel: i.e.,
![]() . The calculation was performed with the
previously listed 2-d Poisson solver using
. The calculation was performed with the
previously listed 2-d Poisson solver using
![]() .
.
