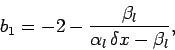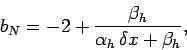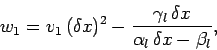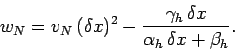Next: An example 1-d Poisson
Up: Poisson's equation
Previous: An example tridiagonal matrix
1-d problem with mixed boundary conditions
Previously, we solved Poisson's equation in one dimension subject
to Dirichlet boundary conditions, which are the simplest
conceivable boundary conditions. Let us now consider the following much more general
set of boundary conditions:
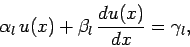 |
(132) |
at 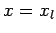 , and
, and
 |
(133) |
at 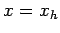 . Here,
. Here, 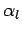 ,
,  , etc., are known constants. The above
boundary conditions are termed mixed, since they are a mixture of Dirichlet and
Neumann boundary conditions.
, etc., are known constants. The above
boundary conditions are termed mixed, since they are a mixture of Dirichlet and
Neumann boundary conditions.
Using the previous notation, the discretized versions of Eq. (132) and (133) are:
respectively.
The above expressions can be rearranged to give
Using Eqs. (115), (136), and (137), the problem can be reduced to
a tridiagonal matrix equation
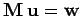 , where the left, center, and
right diagonals of
, where the left, center, and
right diagonals of 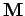 possess the elements
possess the elements 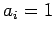 for
for  , with
, with
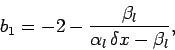 |
(138) |
and 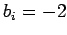 for
for  , plus
, plus
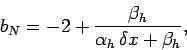 |
(139) |
and 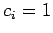 for
for 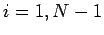 , respectively. The elements of the right-hand side
are
, respectively. The elements of the right-hand side
are
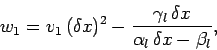 |
(140) |
with
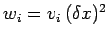 for
for  , and
, and
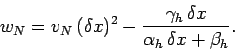 |
(141) |
Our tridiagonal matrix equation can be inverted using the algorithm discussed
previously.



Next: An example 1-d Poisson
Up: Poisson's equation
Previous: An example tridiagonal matrix
Richard Fitzpatrick
2006-03-29
![]() , where the left, center, and
right diagonals of
, where the left, center, and
right diagonals of ![]() possess the elements
possess the elements ![]() for
for ![]() , with
, with