Period-doubling bifurcations

Figure 39: The $v$-coordinate of the Poincaré section of a time-asymptotic orbit plotted against the quality-factor $Q$. Data calculated numerically for $A=1.5$, $\omega =2/3$, $\theta (0)=0$, $v(0)=0$, ${\tt Nacc} = 100$, and $\phi =0$.

Let us now return to Fig. 30. Recall, that as the quality-factor $Q$ is gradually increased, the time-asymptotic orbit of the pendulum through phase-space undergoes a sudden transition, at $Q\simeq 1.245$, from a left-right symmetric, period-1 orbit to a left-favouring, period-1 orbit. What happens if we continue to increase $Q$? Figure 39 is basically a continuation of Fig. 30. It can be seen that as $Q$ is increased the left-favouring, period-1 orbit gradually evolves until a critical value of $Q$, which is about $1.348$, is reached. When $Q$ exceeds this critical value the nature of the orbit undergoes another sudden change: this time from a left-favouring, period-1 orbit to a left-favouring, period-2 orbit. Obviously, the change is indicated by the forking of the curve in Fig. 39. This type of transition is termed a period-doubling bifurcation, since it involves a sudden doubling of the repetition period of the pendulum's time-asymptotic motion.

We can represent period-1 motion schematically as $AAAAAA\cdots$, where $A$ represents a pattern of motion which is repeated every period of the external drive. Likewise, we can represent period-2 motion as $ABABAB\cdots$, where $A$ and $B$ represent distinguishable patterns of motion which are repeated every alternate period of the external drive. A period-doubling bifurcation is represented: $AAAAAA\cdots\rightarrow ABABAB\cdots$. Clearly, all that happens in such a bifurcation is that the pendulum suddenly decides to do something slightly different in alternate periods of the external drive.

Figure 40: Equally spaced (in time) points on a time-asymptotic orbit in phase-space. Data calculated numerically for $Q=1.36$, $A=1.5$, $\omega =2/3$, $\theta (0)=0$, $v(0)=-3$, and ${\tt Nacc} = 100$.

Figure 40 shows the time-asymptotic phase-space orbit of the pendulum calculated for a value of $Q$ somewhat higher than that required to trigger the above mentioned period-doubling bifurcation. It can be seen that the orbit is left-favouring (i.e., it spends the majority of its time on the left-hand side of the plot), and takes the form of a closed curve consisting of two interlocked loops in phase-space. Recall that for period-1 orbits there was only a single closed loop in phase-space. Figure 41 shows the Poincaré section of the orbit shown in Fig. 40. The fact that the section consists of two points confirms that the orbit does indeed correspond to period-2 motion.

Figure 41: The Poincaré section of a time-asymptotic orbit. Data calculated numerically for $Q=1.36$, $A=1.5$, $\omega =2/3$, $\theta (0)=0$, $v(0)=0$, ${\tt Nacc} = 100$, and $\phi =0$.

A period-doubling bifurcation is an example of temporal symmetry breaking. The equations of motion of the pendulum are invariant under the transformation $t\rightarrow t+\tau$, where $\tau$ is the period of the external drive. In the low amplitude (i.e., linear) limit the time-asymptotic motion of the pendulum always respects this symmetry. However, as we have just seen, in the non-linear regime it is possible to obtain solutions which spontaneously break this symmetry. Obviously, motion which repeats itself every two periods of the external drive is not as temporally symmetric as motion which repeats every period of the drive.

Figure 42: The $v$-coordinate of the Poincaré section of a time-asymptotic orbit plotted against the quality-factor $Q$. Data calculated numerically for $A=1.5$, $\omega =2/3$, ${\tt Nacc} = 100$, and $\phi =0$. Data is shown for two sets of initial conditions: $\theta (0)=0$ and $v(0)=0$ (lower branch); and $\theta (0)=0$ and $v(0)=-2$ (upper branch).

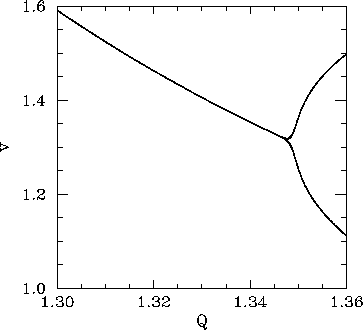
Figure 42 is essentially a continuation of Fig 34. Data is shown for two sets of initial conditions which lead to motions converging on left-favouring (lower branch) and right-favouring (upper branch) periodic attractors. We have already seen that the left-favouring periodic attractor undergoes a period-doubling bifurcation at $Q=1.348$. It is clear from Fig. 42 that the right-favouring attractor undergoes a similar bifurcation at almost exactly the same $Q$-value. This is hardly surprising since, as has already been mentioned, for fixed physics parameters (i.e., $Q$, $A$, $\omega$), the left- and right-favouring attractors are mirror-images of one another.