


Next: Spatial symmetry breaking
Up: The chaotic pendulum
Previous: Validation of numerical solutions
For the sake of definiteness, let us fix the normalized amplitude and frequency of the external
drive to be  and
and 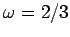 , respectively.24 Furthermore, let us investigate any changes which
may develop in the nature of the
pendulum's time-asymptotic motion
as the quality-factor
, respectively.24 Furthermore, let us investigate any changes which
may develop in the nature of the
pendulum's time-asymptotic motion
as the quality-factor  is varied. Of course, if
is varied. Of course, if  is made sufficiently small
(i.e., if the pendulum is embedded in a sufficiently viscous medium) then we expect the
amplitude of the pendulum's time-asymptotic motion to become low enough that the linear analysis
outlined in Sect. 4.2 remains valid. Indeed, we expect non-linear effects to manifest themselves
as
is made sufficiently small
(i.e., if the pendulum is embedded in a sufficiently viscous medium) then we expect the
amplitude of the pendulum's time-asymptotic motion to become low enough that the linear analysis
outlined in Sect. 4.2 remains valid. Indeed, we expect non-linear effects to manifest themselves
as  is gradually made larger, and the amplitude of the pendulum's motion
consequently increases to such an extent that the
small angle approximation breaks down.
is gradually made larger, and the amplitude of the pendulum's motion
consequently increases to such an extent that the
small angle approximation breaks down.
Figure 28:
Equally spaced (in time) points on a time-asymptotic orbit
in phase-space. Data calculated numerically
for 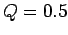 ,
,  ,
, 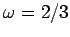 ,
, 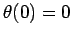 ,
,
 , and
, and
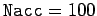 .
.
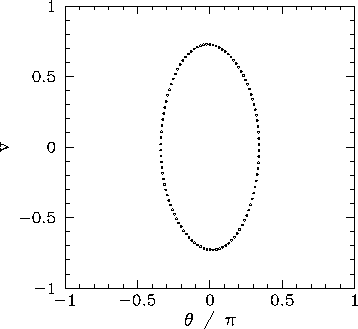 |
Figure 28 shows a time-asymptotic orbit in phase-space
calculated numerically for a case where  is sufficiently
small (i.e.,
is sufficiently
small (i.e., 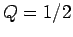 ) that the small angle approximation holds reasonably well. Not surprisingly,
the orbit is very similar to the analytic orbits
described in Sect. 4.2. The fact that the orbit consists
of a single loop, and forms a closed curve in phase-space,
strongly suggests that the corresponding
motion is periodic with the same period as the external drive--we term this type of motion
period-1 motion. More generally, period-
) that the small angle approximation holds reasonably well. Not surprisingly,
the orbit is very similar to the analytic orbits
described in Sect. 4.2. The fact that the orbit consists
of a single loop, and forms a closed curve in phase-space,
strongly suggests that the corresponding
motion is periodic with the same period as the external drive--we term this type of motion
period-1 motion. More generally, period-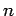 motion consists of motion which
repeats itself exactly every
motion consists of motion which
repeats itself exactly every 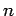 periods of the external drive (and, obviously,
does not repeat itself on any time-scale less than
periods of the external drive (and, obviously,
does not repeat itself on any time-scale less than 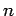 periods). Of course, period-1 motion
is the only allowed time-asymptotic motion in the small angle limit.
periods). Of course, period-1 motion
is the only allowed time-asymptotic motion in the small angle limit.
It would certainly be helpful
to possess a graphical test for period-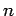 motion. In fact, such a test was developed more than a
hundred years ago by the
French mathematician Henry Poincaré--nowadays, it is called a
Poincaré section in his honour. The idea of a Poincaré section, as applied
to a periodically driven pendulum, is very simple.
As before, we calculate the time-asymptotic motion of the pendulum, and visualize it as a
series of points in
motion. In fact, such a test was developed more than a
hundred years ago by the
French mathematician Henry Poincaré--nowadays, it is called a
Poincaré section in his honour. The idea of a Poincaré section, as applied
to a periodically driven pendulum, is very simple.
As before, we calculate the time-asymptotic motion of the pendulum, and visualize it as a
series of points in  -
-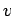 phase-space. However, we only plot one point per period of the external drive. To be more
exact, we only plot a point when
phase-space. However, we only plot one point per period of the external drive. To be more
exact, we only plot a point when
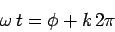 |
(97) |
where 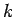 is any integer, and
is any integer, and 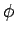 is referred to as the Poincaré phase.
For period-1 motion, in which the motion repeats itself exactly every period of the
external drive, we expect the Poincaré section to consist of only one point
in phase-space (i.e., we expect all of the points to plot on top of one another).
Likewise, for period-2 motion, in which the motion repeats itself exactly every two periods of the
external drive, we expect the Poincaré section to consist of two points
in phase-space (i.e., we expect alternating points to plot on top of one another).
Finally, for period-
is referred to as the Poincaré phase.
For period-1 motion, in which the motion repeats itself exactly every period of the
external drive, we expect the Poincaré section to consist of only one point
in phase-space (i.e., we expect all of the points to plot on top of one another).
Likewise, for period-2 motion, in which the motion repeats itself exactly every two periods of the
external drive, we expect the Poincaré section to consist of two points
in phase-space (i.e., we expect alternating points to plot on top of one another).
Finally, for period-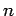 motion we expect the Poincaré section to consist of
motion we expect the Poincaré section to consist of 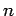 points
in phase-space.
points
in phase-space.
Figure 29:
The Poincaré section of a time-asymptotic
orbit. Data calculated numerically for 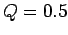 ,
,  ,
, 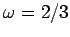 ,
, 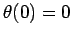 ,
,
 ,
,
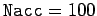 , and
, and 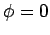 .
.
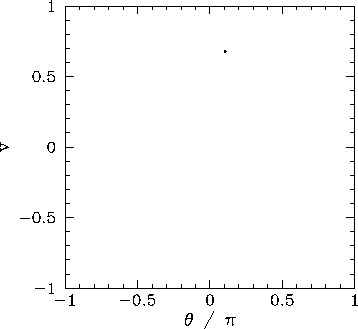 |
Figure 29 displays the Poincaré section of the orbit shown in Fig. 28.
The fact that the section consists of a single point confirms that the motion
displayed in Fig. 28 is indeed period-1 motion.



Next: Spatial symmetry breaking
Up: The chaotic pendulum
Previous: Validation of numerical solutions
Richard Fitzpatrick
2006-03-29


![]() is sufficiently
small (i.e.,
is sufficiently
small (i.e., ![]() ) that the small angle approximation holds reasonably well. Not surprisingly,
the orbit is very similar to the analytic orbits
described in Sect. 4.2. The fact that the orbit consists
of a single loop, and forms a closed curve in phase-space,
strongly suggests that the corresponding
motion is periodic with the same period as the external drive--we term this type of motion
period-1 motion. More generally, period-
) that the small angle approximation holds reasonably well. Not surprisingly,
the orbit is very similar to the analytic orbits
described in Sect. 4.2. The fact that the orbit consists
of a single loop, and forms a closed curve in phase-space,
strongly suggests that the corresponding
motion is periodic with the same period as the external drive--we term this type of motion
period-1 motion. More generally, period-![]() motion consists of motion which
repeats itself exactly every
motion consists of motion which
repeats itself exactly every ![]() periods of the external drive (and, obviously,
does not repeat itself on any time-scale less than
periods of the external drive (and, obviously,
does not repeat itself on any time-scale less than ![]() periods). Of course, period-1 motion
is the only allowed time-asymptotic motion in the small angle limit.
periods). Of course, period-1 motion
is the only allowed time-asymptotic motion in the small angle limit.
![]() motion. In fact, such a test was developed more than a
hundred years ago by the
French mathematician Henry Poincaré--nowadays, it is called a
Poincaré section in his honour. The idea of a Poincaré section, as applied
to a periodically driven pendulum, is very simple.
As before, we calculate the time-asymptotic motion of the pendulum, and visualize it as a
series of points in
motion. In fact, such a test was developed more than a
hundred years ago by the
French mathematician Henry Poincaré--nowadays, it is called a
Poincaré section in his honour. The idea of a Poincaré section, as applied
to a periodically driven pendulum, is very simple.
As before, we calculate the time-asymptotic motion of the pendulum, and visualize it as a
series of points in ![]() -
-![]() phase-space. However, we only plot one point per period of the external drive. To be more
exact, we only plot a point when
phase-space. However, we only plot one point per period of the external drive. To be more
exact, we only plot a point when
