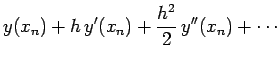 |
|||
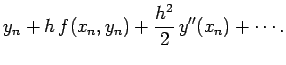 |
(11) |
| (12) |
Note that truncation error would be incurred even if computers performed
floating-point arithmetic operations to infinite accuracy. Unfortunately, computers
do not perform such operations to infinite accuracy. In fact,
a computer is only capable
of storing a floating-point number to a fixed number of
decimal places. For every type of computer, there is a characteristic number,
![]() , which is defined as the smallest number which when added to a number
of order unity gives rise to a new number: i.e., a number
which when taken away from the original number yields a non-zero result.
Every floating-point operation incurs a round-off error of
, which is defined as the smallest number which when added to a number
of order unity gives rise to a new number: i.e., a number
which when taken away from the original number yields a non-zero result.
Every floating-point operation incurs a round-off error of ![]() which arises from the finite accuracy to which floating-point numbers
are stored by the computer. Suppose that we use Euler's method
to integrate our o.d.e. over an
which arises from the finite accuracy to which floating-point numbers
are stored by the computer. Suppose that we use Euler's method
to integrate our o.d.e. over an ![]() -interval of order unity. This
entails
-interval of order unity. This
entails ![]() integration steps, and, therefore,
integration steps, and, therefore, ![]() floating-point operations. If each floating-point operation incurs
an error of
floating-point operations. If each floating-point operation incurs
an error of ![]() , and the errors are simply cumulative, then
the net round-off error is
, and the errors are simply cumulative, then
the net round-off error is ![]() .
.
The total error, ![]() , associated with
integrating our o.d.e. over an
, associated with
integrating our o.d.e. over an ![]() -interval of order unity is (approximately)
the sum of the truncation and round-off errors. Thus,
for Euler's method,
-interval of order unity is (approximately)
the sum of the truncation and round-off errors. Thus,
for Euler's method,
| (13) |
The value of ![]() depends on how many bytes the computer
hardware uses to store floating-point numbers. For
IBM-PC clones, the appropriate value for double precision floating
point numbers is
depends on how many bytes the computer
hardware uses to store floating-point numbers. For
IBM-PC clones, the appropriate value for double precision floating
point numbers is
![]() (this value is specified
in the system header file float.h). It follows that the minimum practical
step-length for Euler's method on such a computer is
(this value is specified
in the system header file float.h). It follows that the minimum practical
step-length for Euler's method on such a computer is
![]() , yielding
a minimum relative integration error of
, yielding
a minimum relative integration error of
![]() . This
level of accuracy is perfectly adequate for most scientific calculations.
Note, however, that the corresponding
. This
level of accuracy is perfectly adequate for most scientific calculations.
Note, however, that the corresponding ![]() value for single precision
floating-point numbers is only
value for single precision
floating-point numbers is only
![]() , yielding a minimum
practical step-length and a minimum relative error for Euler's method of
, yielding a minimum
practical step-length and a minimum relative error for Euler's method of
![]() and
and
![]() , respectively. This level
of accuracy is generally not adequate for scientific calculations, which
explains why such calculations are invariably performed using
double, rather than single, precision floating-point numbers on IBM-PC clones
(and most other types of computer).
, respectively. This level
of accuracy is generally not adequate for scientific calculations, which
explains why such calculations are invariably performed using
double, rather than single, precision floating-point numbers on IBM-PC clones
(and most other types of computer).