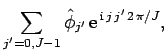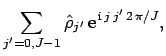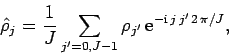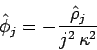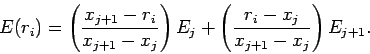Next: An example 1D PIC
Up: Particle-in-cell codes
Previous: Evaluation of electron number
Consider the solution of Poisson's equation:
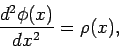 |
(303) |
where
 . Note that
. Note that 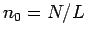 in normalized
units. Let
in normalized
units. Let
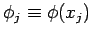 and
and
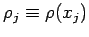 .
We can write
.
We can write
which automatically satisfies the periodic boundary conditions 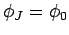 and
and  .
Note that
.
Note that
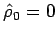 , since
, since
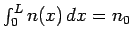 . The other
. The other 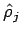 are obtained
from
are obtained
from
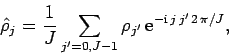 |
(306) |
for 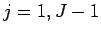 .
The Fourier transformed version of Poisson's equation yields
.
The Fourier transformed version of Poisson's equation yields
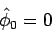 |
(307) |
and
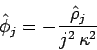 |
(308) |
for 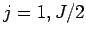 , where
, where
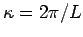 . Finally,
. Finally,
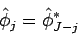 |
(309) |
for  to
to 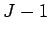 , which ensures that the
, which ensures that the 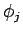 remain real.
The discretized version of Eq. (297) is
remain real.
The discretized version of Eq. (297) is
 |
(310) |
Of course, 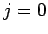 and
and 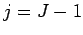 are special cases which can be resolved using the periodic
boundary conditions.
Finally, suppose that the coordinate of the
are special cases which can be resolved using the periodic
boundary conditions.
Finally, suppose that the coordinate of the 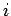 th electron lies between the
th electron lies between the  th and
th and 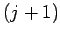 th
grid-points: i.e.,
th
grid-points: i.e.,
 . We can then use linear interpolation to
evaluate the electric field seen by the
. We can then use linear interpolation to
evaluate the electric field seen by the 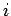 th electron:
th electron:
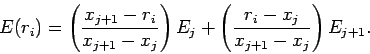 |
(311) |



Next: An example 1D PIC
Up: Particle-in-cell codes
Previous: Evaluation of electron number
Richard Fitzpatrick
2006-03-29