


Next: Magnetic Induction
Up: Magnetism
Previous: Example 8.2: Charged particle
Question: A 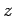 -directed wire of radius
-directed wire of radius 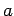 carries a total
carries a total
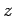 -directed current
-directed current  .
What is the magnetic field distribution, both inside and outside the wire, if the current
is evenly distributed throughout the wire? What is the magnetic field
distribution if the current is
concentrated in a thin layer at the surface of the wire?
.
What is the magnetic field distribution, both inside and outside the wire, if the current
is evenly distributed throughout the wire? What is the magnetic field
distribution if the current is
concentrated in a thin layer at the surface of the wire?
Answer: Since the current distribution possesses
cylindrical symmetry, it is reasonable to suppose that the magnetic field
it generates also possesses cylindrical symmetry. By analogy with the magnetic
field generated by an infinitely thin 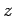 -directed wire, we expect the
magnetic field to circulate in the
-directed wire, we expect the
magnetic field to circulate in the 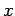 -
-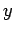 plane in an anti-clockwise direction
(looking against the direction of the current). Let us apply Ampère's circuital
law to a circular loop in the
plane in an anti-clockwise direction
(looking against the direction of the current). Let us apply Ampère's circuital
law to a circular loop in the 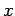 -
-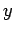 plane which is centred on the centre of
the wire, and is of radius
plane which is centred on the centre of
the wire, and is of radius 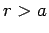 . The magnetic field is everywhere tangential
to the loop, so the line integral of the magnetic field (taken
in an anti-clockwise sense, looking against the direction of the current) is
. The magnetic field is everywhere tangential
to the loop, so the line integral of the magnetic field (taken
in an anti-clockwise sense, looking against the direction of the current) is
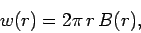
where 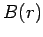 is the magnetic field-strength at radius
is the magnetic field-strength at radius  . According to Ampère's
circuital law, this line integral is equal to
. According to Ampère's
circuital law, this line integral is equal to 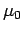 times the total current enclosed by
the loop. The total current is clearly
times the total current enclosed by
the loop. The total current is clearly  , since the loop lies outside the wire.
Thus,
, since the loop lies outside the wire.
Thus,
giving
for 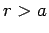 . This is exactly the same field distribution as that generated by an
infinitely thin wire carrying the current
. This is exactly the same field distribution as that generated by an
infinitely thin wire carrying the current  . Thus, we conclude that the magnetic field generated outside
a cylindrically symmetric
. Thus, we conclude that the magnetic field generated outside
a cylindrically symmetric  -directed current distribution is the same as if all of the
current were concentrated at the centre of the distribution.
Let us now apply Ampère's circuital
law to a circular loop which is of radius
-directed current distribution is the same as if all of the
current were concentrated at the centre of the distribution.
Let us now apply Ampère's circuital
law to a circular loop which is of radius 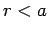 . The line integral
of the magnetic field around this loop is simply
. The line integral
of the magnetic field around this loop is simply
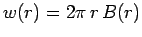 .
However, the current enclosed by the loop is equal to
.
However, the current enclosed by the loop is equal to  times the ratio of
the area of the loop to the cross-sectional area of the wire (since the
current is evenly distributed throughout the wire). Thus, Ampère's
law yields
times the ratio of
the area of the loop to the cross-sectional area of the wire (since the
current is evenly distributed throughout the wire). Thus, Ampère's
law yields
which gives
Clearly, the field inside the wire increases linearly with increasing distance
from the centre of the wire.
If the current flows along the outside of the wire then the magnetic
field distribution exterior to the wire is exactly the same as that
described above. However, there is no field inside the wire. This
follows immediately from Ampère's circuital
law because the current enclosed by a circular loop whose radius is less than
the radius of the wire is clearly zero.



Next: Magnetic Induction
Up: Magnetism
Previous: Example 8.2: Charged particle
Richard Fitzpatrick
2007-07-14