


Next: Origin of Permanent Magnetism
Up: Magnetism
Previous: Ampère's Circuital Law
Magnetic Field of a Solenoid
A solenoid is a tightly wound helical coil of wire whose diameter is small compared
to its length. The magnetic field generated in the centre, or core,
of a current carrying solenoid
is essentially uniform, and is directed along the axis of the solenoid.
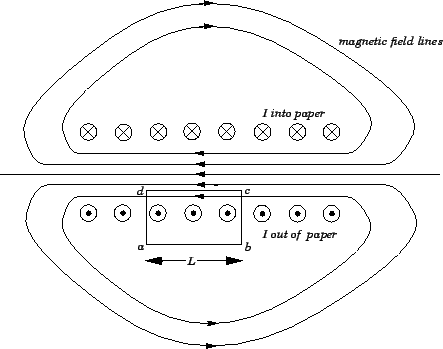
Outside the solenoid, the magnetic field is far weaker. Figure 27 shows
(rather schematically) the magnetic field generated by a typical solenoid.
The solenoid is wound from a single helical wire which carries a current  .
The winding is sufficiently tight that each turn of the solenoid is well
approximated as
a circular wire loop, lying in the plane perpendicular to the axis of
the solenoid, which carries a current
.
The winding is sufficiently tight that each turn of the solenoid is well
approximated as
a circular wire loop, lying in the plane perpendicular to the axis of
the solenoid, which carries a current  . Suppose that there
are
. Suppose that there
are 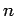 such turns per unit axial length of the solenoid. What is the
magnitude of the magnetic field in the core of the solenoid?
such turns per unit axial length of the solenoid. What is the
magnitude of the magnetic field in the core of the solenoid?
Figure 27:
A solenoid.
 |
In order to answer this question, let us apply Ampère's circuital
law to the rectangular loop 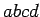 . We must first find the line integral
of the magnetic field around
. We must first find the line integral
of the magnetic field around 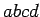 . Along
. Along 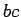 and
and 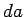 the magnetic field
is essentially perpendicular to the loop, so there is no contribution to
the line integral from these sections of the loop.
Along
the magnetic field
is essentially perpendicular to the loop, so there is no contribution to
the line integral from these sections of the loop.
Along 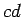 the magnetic field is approximately uniform,
of magnitude
the magnetic field is approximately uniform,
of magnitude 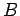 , say, and is directed parallel to the loop. Thus, the
contribution to the line integral from this section of the loop
is
, say, and is directed parallel to the loop. Thus, the
contribution to the line integral from this section of the loop
is 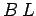 , where
, where  is the length of
is the length of 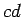 .
Along
.
Along 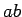 the magnetic field-strength is essentially negligible, so
this section of the loop makes no contribution to the line
integral. It follows that the line integral of the
magnetic field around
the magnetic field-strength is essentially negligible, so
this section of the loop makes no contribution to the line
integral. It follows that the line integral of the
magnetic field around 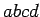 is simply
is simply
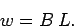 |
(178) |
By Ampère's circuital law, this line integral is equal to 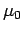 times the algebraic sum of
the currents which flow through the loop
times the algebraic sum of
the currents which flow through the loop  . Since the length of the
loop along the axis of the solenoid is
. Since the length of the
loop along the axis of the solenoid is  , the loop intersects
, the loop intersects 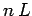 turns of the solenoid, each carrying a current
turns of the solenoid, each carrying a current  . Thus, the total
current which flows through the loop is
. Thus, the total
current which flows through the loop is 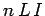 . This current counts as
a positive current since if we look against the direction of the
currents flowing in each turn
(i.e., into the page in the figure), the loop
. This current counts as
a positive current since if we look against the direction of the
currents flowing in each turn
(i.e., into the page in the figure), the loop  circulates
these currents in an anti-clockwise direction. Ampère's circuital law yields
circulates
these currents in an anti-clockwise direction. Ampère's circuital law yields
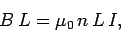 |
(179) |
which reduces to
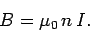 |
(180) |
Thus, the magnetic field in the core of a solenoid is directly
proportional to the product of the
current flowing around the solenoid and the number
of turns per unit length of the solenoid. This, result is exact in the
limit in which the length of the solenoid is very much greater than its diameter.



Next: Origin of Permanent Magnetism
Up: Magnetism
Previous: Ampère's Circuital Law
Richard Fitzpatrick
2007-07-14

![]() . We must first find the line integral
of the magnetic field around
. We must first find the line integral
of the magnetic field around ![]() . Along
. Along ![]() and
and ![]() the magnetic field
is essentially perpendicular to the loop, so there is no contribution to
the line integral from these sections of the loop.
Along
the magnetic field
is essentially perpendicular to the loop, so there is no contribution to
the line integral from these sections of the loop.
Along ![]() the magnetic field is approximately uniform,
of magnitude
the magnetic field is approximately uniform,
of magnitude ![]() , say, and is directed parallel to the loop. Thus, the
contribution to the line integral from this section of the loop
is
, say, and is directed parallel to the loop. Thus, the
contribution to the line integral from this section of the loop
is ![]() , where
, where ![]() is the length of
is the length of ![]() .
Along
.
Along ![]() the magnetic field-strength is essentially negligible, so
this section of the loop makes no contribution to the line
integral. It follows that the line integral of the
magnetic field around
the magnetic field-strength is essentially negligible, so
this section of the loop makes no contribution to the line
integral. It follows that the line integral of the
magnetic field around ![]() is simply
is simply