

Next: The Lorentz Force
Up: Magnetism
Previous: Ampère's Experiments
Magnetic fields, like electric fields, are completely
superposable. So, if
a field 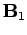 is generated by a current
is generated by a current 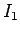 flowing through some circuit,
and a field
flowing through some circuit,
and a field 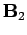 is generated by a current
is generated by a current 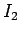 flowing through another
circuit, then when the currents
flowing through another
circuit, then when the currents 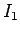 and
and 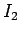 flow through both circuits
simultaneously the generated magnetic field is
flow through both circuits
simultaneously the generated magnetic field is
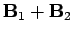 .
This is true at all points in space.
.
This is true at all points in space.
Figure 22:
Two parallel current carrying wires.
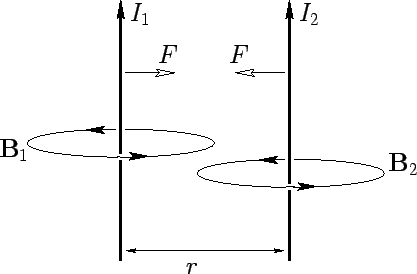 |
Consider two parallel wires separated by a perpendicular distance 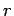 ,
and carrying electric currents
,
and carrying electric currents 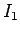 and
and 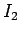 , respectively. The magnetic field-strength at the second wire due to the current flowing in the first wire
is
, respectively. The magnetic field-strength at the second wire due to the current flowing in the first wire
is
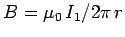 . This field is orientated at right-angles to the second
wire, so the force per unit length exerted on the second wire is
. This field is orientated at right-angles to the second
wire, so the force per unit length exerted on the second wire is
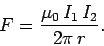 |
(156) |
This follows from Eq. (152), which is valid for continuous wires as well as short
test wires. The force acting on the second wire is directed radially inwards towards
the first wire. The magnetic field-strength at the first wire due to the
current flowing in the second wire is
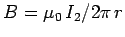 . This field
is orientated at right-angles to the first wire, so the force per unit length acting
on the first wire is equal and opposite to that acting on the second wire,
according to Eq. (152). Equation (156) is called Ampère's law.
. This field
is orientated at right-angles to the first wire, so the force per unit length acting
on the first wire is equal and opposite to that acting on the second wire,
according to Eq. (152). Equation (156) is called Ampère's law.
Incidentally, Eq. (156) is the basis of the official SI definition of the
ampere, which is:
One ampere is the magnitude of the current which, when flowing in
each of two long parallel wires one meter apart, results in a force
between the wires of exactly
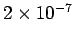 N per meter of length.
N per meter of length.
We can see that it is no accident that the constant 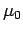 has the
numerical value of exactly
has the
numerical value of exactly
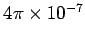 .
The SI system of units is based on four standard units: the meter,
the kilogram, the second, and the ampere. Hence, the SI system is
sometime referred to as the MKSA system. All other units can be derived
from these four standard units. For instance, a coulomb is equivalent to
an ampere-second. You may be wondering why the ampere is the standard
electrical unit, rather than the coulomb, since the latter unit is
clearly more fundamental than the former. The answer is simple. It is very difficult
to measure charge accurately, whereas it is easy to accurately measure electric
current. Clearly, it makes sense to define a standard unit in terms
of something which is easily measurable, rather than something which is
difficult to measure.
.
The SI system of units is based on four standard units: the meter,
the kilogram, the second, and the ampere. Hence, the SI system is
sometime referred to as the MKSA system. All other units can be derived
from these four standard units. For instance, a coulomb is equivalent to
an ampere-second. You may be wondering why the ampere is the standard
electrical unit, rather than the coulomb, since the latter unit is
clearly more fundamental than the former. The answer is simple. It is very difficult
to measure charge accurately, whereas it is easy to accurately measure electric
current. Clearly, it makes sense to define a standard unit in terms
of something which is easily measurable, rather than something which is
difficult to measure.


Next: The Lorentz Force
Up: Magnetism
Previous: Ampère's Experiments
Richard Fitzpatrick
2007-07-14

N per meter of length.