


Next: Resistance and Resistivity
Up: Electric Current
Previous: Electric Circuits
Consider, again, a simple circuit in which a steady current  flows through
a single conducting wire connecting the positive and negative terminals
of a battery of voltage
flows through
a single conducting wire connecting the positive and negative terminals
of a battery of voltage 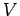 . What is the relationship between the current
. What is the relationship between the current
 flowing in the wire and the potential difference
flowing in the wire and the potential difference 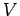 applied across
the two ends of the wire by the battery? If we were to investigate this relationship experimentally we would quickly conclude that the current
applied across
the two ends of the wire by the battery? If we were to investigate this relationship experimentally we would quickly conclude that the current
 is directly proportional to the potential difference
is directly proportional to the potential difference 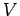 . In other words,
. In other words,
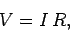 |
(126) |
where the constant of proportionality 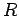 is termed the (electrical) resistance
of the wire. The above formula is called Ohm's law after its
discoverer, the early nineteenth century German physicist Georg Simon Ohm.
The unit of electrical resistance is the ohm (
is termed the (electrical) resistance
of the wire. The above formula is called Ohm's law after its
discoverer, the early nineteenth century German physicist Georg Simon Ohm.
The unit of electrical resistance is the ohm (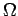 ), which is
equivalent to a volt per ampere:
), which is
equivalent to a volt per ampere:
 |
(127) |
There is a slight discrepancy between what we are saying
now, and what we said earlier. In Sect. 5, we maintained that the
electric field inside a conductor is zero. However, if there is a potential difference
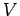 between the beginning and the end of a conducting wire, as described above,
then there must be an
electric field running along the length of the wire. In fact, if the
wire is straight, and the electric potential decreases uniformly with
distance traveled along the wire, then the longitudinal electric
field-strength is given by
between the beginning and the end of a conducting wire, as described above,
then there must be an
electric field running along the length of the wire. In fact, if the
wire is straight, and the electric potential decreases uniformly with
distance traveled along the wire, then the longitudinal electric
field-strength is given by 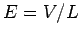 (see Sect. 5.3), where
(see Sect. 5.3), where  is the length of the wire.
The earlier result that there is zero electric field inside a
conductor is equivalent to saying that conductors possess zero electrical
resistance. This follows because if
is the length of the wire.
The earlier result that there is zero electric field inside a
conductor is equivalent to saying that conductors possess zero electrical
resistance. This follows because if 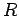 is zero then the electric field, and, hence, the potential
difference
is zero then the electric field, and, hence, the potential
difference 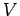 , must be zero, otherwise an infinite current would flow
according to Ohm's law. It turns out that good conductors (i.e.,
copper, silver, aluminium, and most other metals) possess
non-zero electrical
resistances. However, these resistances are generally so small that
if we were to connect the terminals of a battery together using a
wire fashioned out of a good conductor then the current which would flow
in the wire, according to Ohm's law, would be so large that it would
damage both the wire and the battery. We usually call such a circuit
a short-circuit. In order to prevent excessively large currents from
flowing, conventional electric circuits contain components, called resistors,
whose electrical resistance is many orders of magnitude greater than that
of the conducting wires in the circuit. When we apply Ohm's
law,
, must be zero, otherwise an infinite current would flow
according to Ohm's law. It turns out that good conductors (i.e.,
copper, silver, aluminium, and most other metals) possess
non-zero electrical
resistances. However, these resistances are generally so small that
if we were to connect the terminals of a battery together using a
wire fashioned out of a good conductor then the current which would flow
in the wire, according to Ohm's law, would be so large that it would
damage both the wire and the battery. We usually call such a circuit
a short-circuit. In order to prevent excessively large currents from
flowing, conventional electric circuits contain components, called resistors,
whose electrical resistance is many orders of magnitude greater than that
of the conducting wires in the circuit. When we apply Ohm's
law, 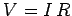 , to a circuit, we usually only count the net resistance
, to a circuit, we usually only count the net resistance 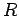 of
all the
resistors in the circuit, and neglect the resistances of the interconnecting
wires. This means that all of the major drops in electric potential, as we
travel around the circuit from one terminal of the battery to the other,
take place inside the resistors. The drop in potential in the conducting
wires themselves is usually negligible.
Thus, to all intents and purposes, good conductors, and wires
made out of good conductors, act as if they
have zero resistance, and contain zero electric field.
of
all the
resistors in the circuit, and neglect the resistances of the interconnecting
wires. This means that all of the major drops in electric potential, as we
travel around the circuit from one terminal of the battery to the other,
take place inside the resistors. The drop in potential in the conducting
wires themselves is usually negligible.
Thus, to all intents and purposes, good conductors, and wires
made out of good conductors, act as if they
have zero resistance, and contain zero electric field.



Next: Resistance and Resistivity
Up: Electric Current
Previous: Electric Circuits
Richard Fitzpatrick
2007-07-14
![]() between the beginning and the end of a conducting wire, as described above,
then there must be an
electric field running along the length of the wire. In fact, if the
wire is straight, and the electric potential decreases uniformly with
distance traveled along the wire, then the longitudinal electric
field-strength is given by
between the beginning and the end of a conducting wire, as described above,
then there must be an
electric field running along the length of the wire. In fact, if the
wire is straight, and the electric potential decreases uniformly with
distance traveled along the wire, then the longitudinal electric
field-strength is given by ![]() (see Sect. 5.3), where
(see Sect. 5.3), where ![]() is the length of the wire.
The earlier result that there is zero electric field inside a
conductor is equivalent to saying that conductors possess zero electrical
resistance. This follows because if
is the length of the wire.
The earlier result that there is zero electric field inside a
conductor is equivalent to saying that conductors possess zero electrical
resistance. This follows because if ![]() is zero then the electric field, and, hence, the potential
difference
is zero then the electric field, and, hence, the potential
difference ![]() , must be zero, otherwise an infinite current would flow
according to Ohm's law. It turns out that good conductors (i.e.,
copper, silver, aluminium, and most other metals) possess
non-zero electrical
resistances. However, these resistances are generally so small that
if we were to connect the terminals of a battery together using a
wire fashioned out of a good conductor then the current which would flow
in the wire, according to Ohm's law, would be so large that it would
damage both the wire and the battery. We usually call such a circuit
a short-circuit. In order to prevent excessively large currents from
flowing, conventional electric circuits contain components, called resistors,
whose electrical resistance is many orders of magnitude greater than that
of the conducting wires in the circuit. When we apply Ohm's
law,
, must be zero, otherwise an infinite current would flow
according to Ohm's law. It turns out that good conductors (i.e.,
copper, silver, aluminium, and most other metals) possess
non-zero electrical
resistances. However, these resistances are generally so small that
if we were to connect the terminals of a battery together using a
wire fashioned out of a good conductor then the current which would flow
in the wire, according to Ohm's law, would be so large that it would
damage both the wire and the battery. We usually call such a circuit
a short-circuit. In order to prevent excessively large currents from
flowing, conventional electric circuits contain components, called resistors,
whose electrical resistance is many orders of magnitude greater than that
of the conducting wires in the circuit. When we apply Ohm's
law, ![]() , to a circuit, we usually only count the net resistance
, to a circuit, we usually only count the net resistance ![]() of
all the
resistors in the circuit, and neglect the resistances of the interconnecting
wires. This means that all of the major drops in electric potential, as we
travel around the circuit from one terminal of the battery to the other,
take place inside the resistors. The drop in potential in the conducting
wires themselves is usually negligible.
Thus, to all intents and purposes, good conductors, and wires
made out of good conductors, act as if they
have zero resistance, and contain zero electric field.
of
all the
resistors in the circuit, and neglect the resistances of the interconnecting
wires. This means that all of the major drops in electric potential, as we
travel around the circuit from one terminal of the battery to the other,
take place inside the resistors. The drop in potential in the conducting
wires themselves is usually negligible.
Thus, to all intents and purposes, good conductors, and wires
made out of good conductors, act as if they
have zero resistance, and contain zero electric field.