


Next: Breakdown
Up: Capacitance
Previous: Capacitance
Consider a hollow metal sphere mounted on an insulating stand. The sphere is
initially grounded so that no excess charge remains on it. Suppose that
we introduce a metal ball, suspended on an insulating thread,
through a small hole in the sphere,
and then fill in the hole with a metal plug. Let the ball carry a charge
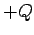 . What distribution of charge is induced on the hollow sphere as a result
of introducing the positive charge into the cavity?
. What distribution of charge is induced on the hollow sphere as a result
of introducing the positive charge into the cavity?
To answer this question we make use of Gauss' law (see Sect. 4.2)
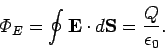 |
(100) |
Assuming that the metal ball is placed at the centre of the hollow sphere,
we can use symmetry arguments to deduce that the electric field
depends only on the radial distance  from the centre,
and is everywhere directed radially away from the ball. Let us choose a
spherical gaussian surface, centred on the ball, which runs through the
interior of the hollow metal sphere. We know that the electric field inside a
conductor is everywhere zero (see Sect. 4.6), so the electric flux
from the centre,
and is everywhere directed radially away from the ball. Let us choose a
spherical gaussian surface, centred on the ball, which runs through the
interior of the hollow metal sphere. We know that the electric field inside a
conductor is everywhere zero (see Sect. 4.6), so the electric flux
 through the surface is also zero. It follows from Gauss' law that
zero net charge is enclosed by the surface. Now, there is a
charge
through the surface is also zero. It follows from Gauss' law that
zero net charge is enclosed by the surface. Now, there is a
charge  on the ball at the centre of the hollow sphere, so there must be an equal and
opposite
charge
on the ball at the centre of the hollow sphere, so there must be an equal and
opposite
charge 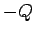 distributed over the interior surface of the sphere
(recall that any charge carried on a conductor must reside on its surface).
Furthermore, since the sphere is insulated, and was initially uncharged, a
charge
distributed over the interior surface of the sphere
(recall that any charge carried on a conductor must reside on its surface).
Furthermore, since the sphere is insulated, and was initially uncharged, a
charge 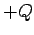 must be distributed over its exterior surface. Thus, when
the charge
must be distributed over its exterior surface. Thus, when
the charge 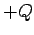 is introduced into the centre of the sphere, there is
a redistribution of charge in the sphere such that a positive charge
is introduced into the centre of the sphere, there is
a redistribution of charge in the sphere such that a positive charge 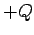 is repelled to its exterior surface, leaving a negative charge
is repelled to its exterior surface, leaving a negative charge 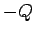 on the interior surface. (In actuality, free electrons are attracted to
the interior surface, exposing positive charges on the exterior surface).
Further use of Gauss' law shows that the electric field between the charged ball and
the interior surface of the sphere is the same as that generated by a point
charge
on the interior surface. (In actuality, free electrons are attracted to
the interior surface, exposing positive charges on the exterior surface).
Further use of Gauss' law shows that the electric field between the charged ball and
the interior surface of the sphere is the same as that generated by a point
charge
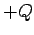 located at the centre of the sphere. Likewise, for the electric
field exterior to the sphere. The electric field inside the conducting
sphere is, of course, zero.
located at the centre of the sphere. Likewise, for the electric
field exterior to the sphere. The electric field inside the conducting
sphere is, of course, zero.
Suppose, finally, that the ball is moved so that it touches the inside of the hollow
sphere. The charge 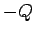 on the interior surface of the sphere cancels the
charge
on the interior surface of the sphere cancels the
charge 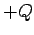 on the ball, leaving the charge
on the ball, leaving the charge 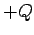 distributed over
its exterior surface. Thus, the effect of touching the
ball to the inside of the sphere is to transfer the charge
distributed over
its exterior surface. Thus, the effect of touching the
ball to the inside of the sphere is to transfer the charge 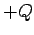 from
the ball to the exterior surface of the sphere. In principle, we
can repeat this process, again and again, until a very large amount of charge
is accumulated on the outside of the
sphere. The idea of transferring charge from one conductor
to another by means of internal contact is the theoretical
basis of the Van de Graaff
generator. In this type of device, charge is continuously transmitted to a conducting sphere by
means of a moving belt charged by friction.
from
the ball to the exterior surface of the sphere. In principle, we
can repeat this process, again and again, until a very large amount of charge
is accumulated on the outside of the
sphere. The idea of transferring charge from one conductor
to another by means of internal contact is the theoretical
basis of the Van de Graaff
generator. In this type of device, charge is continuously transmitted to a conducting sphere by
means of a moving belt charged by friction.



Next: Breakdown
Up: Capacitance
Previous: Capacitance
Richard Fitzpatrick
2007-07-14
![]() on the interior surface of the sphere cancels the
charge
on the interior surface of the sphere cancels the
charge ![]() on the ball, leaving the charge
on the ball, leaving the charge ![]() distributed over
its exterior surface. Thus, the effect of touching the
ball to the inside of the sphere is to transfer the charge
distributed over
its exterior surface. Thus, the effect of touching the
ball to the inside of the sphere is to transfer the charge ![]() from
the ball to the exterior surface of the sphere. In principle, we
can repeat this process, again and again, until a very large amount of charge
is accumulated on the outside of the
sphere. The idea of transferring charge from one conductor
to another by means of internal contact is the theoretical
basis of the Van de Graaff
generator. In this type of device, charge is continuously transmitted to a conducting sphere by
means of a moving belt charged by friction.
from
the ball to the exterior surface of the sphere. In principle, we
can repeat this process, again and again, until a very large amount of charge
is accumulated on the outside of the
sphere. The idea of transferring charge from one conductor
to another by means of internal contact is the theoretical
basis of the Van de Graaff
generator. In this type of device, charge is continuously transmitted to a conducting sphere by
means of a moving belt charged by friction.