


Next: Electric Potential and Electric
Up: Electric Potential
Previous: Electric Potential Energy
Consider a charge 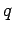 placed in an electric field generated by fixed charges.
Let us chose some arbitrary reference point
placed in an electric field generated by fixed charges.
Let us chose some arbitrary reference point  in the field.
At this point, the electric
potential energy of the charge is defined to be zero. This
uniquely specifies the
electric potential energy of the charge at every other point in the field.
For instance, the electric potential energy
in the field.
At this point, the electric
potential energy of the charge is defined to be zero. This
uniquely specifies the
electric potential energy of the charge at every other point in the field.
For instance, the electric potential energy 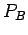 at some point
at some point 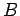 is
simply the work
is
simply the work 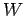 done in moving the charge from
done in moving the charge from  to
to 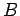 along any path. Now,
along any path. Now,
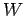 can be calculated using Eq. (78). It is clear, from this equation, that
can be calculated using Eq. (78). It is clear, from this equation, that
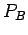 depends both on the particular charge
depends both on the particular charge 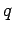 which we place in the
field, and the magnitude and direction of the electric field along the chosen route between points
which we place in the
field, and the magnitude and direction of the electric field along the chosen route between points  and
and 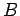 . However, it is also clear that
. However, it is also clear that
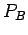 is directly proportional to the magnitude of the
charge
is directly proportional to the magnitude of the
charge 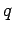 . Thus, if the electric
potential energy of a charge
. Thus, if the electric
potential energy of a charge 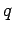 at point
at point 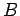 is
is 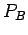 then the electric potential
energy of a charge
then the electric potential
energy of a charge 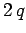 at the same point is
at the same point is 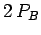 . We can exploit
this fact to define a quantity known as the electric potential. The
difference in electric potential between two points
. We can exploit
this fact to define a quantity known as the electric potential. The
difference in electric potential between two points 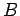 and
and  in an electric
field is simply the work done in moving some charge between the two points
divided by the magnitude of the charge. Thus,
in an electric
field is simply the work done in moving some charge between the two points
divided by the magnitude of the charge. Thus,
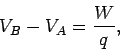 |
(80) |
where 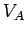 denotes the electric potential at point
denotes the electric potential at point  , etc. This definition
uniquely defines the difference in electric potential between points
, etc. This definition
uniquely defines the difference in electric potential between points  and
and
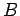 , but the absolute value of the potential at point
, but the absolute value of the potential at point  remains arbitrary.
We can therefore, without loss of generality, set the potential at point
remains arbitrary.
We can therefore, without loss of generality, set the potential at point  equal to
zero. It follows that the potential energy of a charge
equal to
zero. It follows that the potential energy of a charge 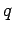 at some point
at some point 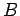 is simply the product of the magnitude of the charge and the electric
potential
is simply the product of the magnitude of the charge and the electric
potential 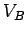 at that point:
at that point:
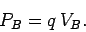 |
(81) |
It is clear, from a comparison of Eqs. (78) and (79), that the electric
potential at point 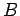 (relative to point
(relative to point  ) is solely a property of the
electric field, and is, therefore, the same for any charge placed at that point.
We shall see exactly how the electric potential is related to the electric
field later on.
) is solely a property of the
electric field, and is, therefore, the same for any charge placed at that point.
We shall see exactly how the electric potential is related to the electric
field later on.
The dimensions of electric potential are work (or energy) per unit charge.
The units of electric potential are, therefore, joules per coulomb (
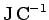 ).
A joule per coulomb is usually referred to as a volt (V): i.e.,
).
A joule per coulomb is usually referred to as a volt (V): i.e.,
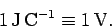 |
(82) |
Thus, the
alternative (and more conventional) units of electric potential are volts.
The difference in electric potential between two points in an electric field
is usually referred to as the potential difference, or even the difference
in ``voltage,''
between the two points.
A battery is a convenient tool for generating a difference in electric potential
between two points in space. For instance, a twelve volt (12V) battery
generates an electric field, usually via some chemical process, which is such
that the potential difference 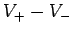 between its positive and negative
terminals is twelve volts. This means that in order to move a
positive charge of 1 coulomb from the negative to the positive terminal of
the battery we must do 12 joules of work against the electric field. (This is
true irrespective of the route taken between the two terminals).
This implies that the electric field must be directed predominately from the
positive to the negative terminal.
between its positive and negative
terminals is twelve volts. This means that in order to move a
positive charge of 1 coulomb from the negative to the positive terminal of
the battery we must do 12 joules of work against the electric field. (This is
true irrespective of the route taken between the two terminals).
This implies that the electric field must be directed predominately from the
positive to the negative terminal.
More generally, in order to move a charge 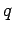 through a potential difference
through a potential difference 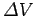 we must do work
we must do work
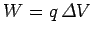 , and the electric potential energy
of the charge increases by an amount
, and the electric potential energy
of the charge increases by an amount
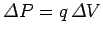 in the
process. Thus, if we move an electron, for which
in the
process. Thus, if we move an electron, for which
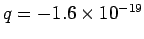 C,
through a potential difference of minus 1 volt then we must do
C,
through a potential difference of minus 1 volt then we must do
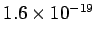 joules of work. This amount of work (or energy) is
called an electronvolt (eV): i.e.,
joules of work. This amount of work (or energy) is
called an electronvolt (eV): i.e.,
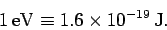 |
(83) |
The electronvolt is a convenient measure of energy in atomic physics.
For instance, the energy required to
break up a hydrogen atom into a free electron and a free proton is 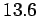 eV.
eV.



Next: Electric Potential and Electric
Up: Electric Potential
Previous: Electric Potential Energy
Richard Fitzpatrick
2007-07-14
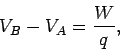
![]() ).
A joule per coulomb is usually referred to as a volt (V): i.e.,
).
A joule per coulomb is usually referred to as a volt (V): i.e.,
![]() between its positive and negative
terminals is twelve volts. This means that in order to move a
positive charge of 1 coulomb from the negative to the positive terminal of
the battery we must do 12 joules of work against the electric field. (This is
true irrespective of the route taken between the two terminals).
This implies that the electric field must be directed predominately from the
positive to the negative terminal.
between its positive and negative
terminals is twelve volts. This means that in order to move a
positive charge of 1 coulomb from the negative to the positive terminal of
the battery we must do 12 joules of work against the electric field. (This is
true irrespective of the route taken between the two terminals).
This implies that the electric field must be directed predominately from the
positive to the negative terminal.
![]() through a potential difference
through a potential difference ![]() we must do work
we must do work
![]() , and the electric potential energy
of the charge increases by an amount
, and the electric potential energy
of the charge increases by an amount
![]() in the
process. Thus, if we move an electron, for which
in the
process. Thus, if we move an electron, for which
![]() C,
through a potential difference of minus 1 volt then we must do
C,
through a potential difference of minus 1 volt then we must do
![]() joules of work. This amount of work (or energy) is
called an electronvolt (eV): i.e.,
joules of work. This amount of work (or energy) is
called an electronvolt (eV): i.e.,