


Next: Electric Potential
Up: Gauss' Law
Previous: Worked Examples
Question: An insulating sphere of radius 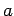 carries a total
charge
carries a total
charge 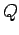 which is uniformly distributed over the volume of the
sphere. Use Gauss' law to find the electric field distribution both
inside and outside the sphere.
which is uniformly distributed over the volume of the
sphere. Use Gauss' law to find the electric field distribution both
inside and outside the sphere.
Solution:
By symmetry, we expect the electric field generated by a spherically symmetric
charge distribution to point radially towards, or away from, the
center of the distribution, and to depend only on
the radial distance  from this point. Consider a
gaussian surface which is a sphere of radius
from this point. Consider a
gaussian surface which is a sphere of radius  , centred on the centre of the
charge distribution. Gauss' law gives
, centred on the centre of the
charge distribution. Gauss' law gives
where
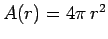 is the area of the surface,
is the area of the surface, 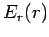 the radial electric
field-strength at radius
the radial electric
field-strength at radius  , and
, and 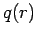 the total charge enclosed by the
surface. It is easily seen that
the total charge enclosed by the
surface. It is easily seen that
Thus,
Clearly, the electric field-strength is proportional to  inside the
sphere, but falls off like
inside the
sphere, but falls off like  outside the sphere.
outside the sphere.



Next: Electric Potential
Up: Gauss' Law
Previous: Worked Examples
Richard Fitzpatrick
2007-07-14
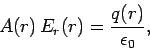
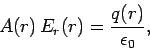
![\begin{displaymath}
q(r) =
\left\{\begin{array}{lcl}
Q&\mbox{\hspace{1cm}}&r\geq a\\ [0.5ex]
Q\,(r/a)^3&&r<a
\end{array}\right..
\end{displaymath}](img357.png)
![\begin{displaymath}
E_r(r) =
\left\{\begin{array}{lcl}
\frac{Q}{4\pi\epsilon_0\,...
...5ex]
\frac{Q\,r}{4\pi\epsilon_0\,a^3}&&r<a
\end{array}\right..
\end{displaymath}](img358.png)