The graphical method of locating the image produced by a concave mirror consists of drawing light-rays emanating from key points on the object, and finding where these rays are brought to a focus by the mirror. This task can be accomplished using just four simple rules:
Consider an object ![]() which is placed a distance
which is placed a distance ![]() from a concave spherical mirror, as shown in Fig. 71. For the sake of
definiteness, let us suppose that the object distance
from a concave spherical mirror, as shown in Fig. 71. For the sake of
definiteness, let us suppose that the object distance ![]() is
greater than the focal length
is
greater than the focal length ![]() of the mirror. Each point
on the object is assumed to radiate light-rays in all directions.
Consider four light-rays emanating from the tip
of the mirror. Each point
on the object is assumed to radiate light-rays in all directions.
Consider four light-rays emanating from the tip ![]() of the
object which strike the mirror, as shown in the figure.
The reflected rays are constructed using rules 1-4 above, and the
rays are labelled accordingly. It can be seen
that the reflected rays all come together at some point
of the
object which strike the mirror, as shown in the figure.
The reflected rays are constructed using rules 1-4 above, and the
rays are labelled accordingly. It can be seen
that the reflected rays all come together at some point ![]() . Thus,
. Thus,
![]() is the image of
is the image of ![]() (i.e., if we were to place a small
projection screen at
(i.e., if we were to place a small
projection screen at ![]() then we would see an image of the tip on the
screen). As is easily demonstrated, rays emanating from other parts
of the object are brought into focus in the vicinity of
then we would see an image of the tip on the
screen). As is easily demonstrated, rays emanating from other parts
of the object are brought into focus in the vicinity of ![]() such
that a complete image of the object is produced between
such
that a complete image of the object is produced between
![]() and
and ![]() (obviously, point
(obviously, point ![]() is the image of point
is the image of point ![]() ).
This image could be viewed by
projecting it onto a screen placed between points
).
This image could be viewed by
projecting it onto a screen placed between points
![]() and
and ![]() . Such an image is termed a real image.
Note that the image
. Such an image is termed a real image.
Note that the image ![]() would also be directly
visible to an observer looking
straight at the mirror from a distance greater than the image
distance
would also be directly
visible to an observer looking
straight at the mirror from a distance greater than the image
distance ![]() (since the observer's eyes could not
tell that the light-rays
diverging from the image were in anyway different from those
which would emanate from a real object). According to the figure, the image is inverted with respect to the object, and is
also magnified.
(since the observer's eyes could not
tell that the light-rays
diverging from the image were in anyway different from those
which would emanate from a real object). According to the figure, the image is inverted with respect to the object, and is
also magnified.
Figure 72 shows what happens when the object distance ![]() is less than the focal length
is less than the focal length ![]() . In this case, the image
appears to an observer looking straight
at the mirror to be located behind the mirror.
For instance, rays emanating from the tip
. In this case, the image
appears to an observer looking straight
at the mirror to be located behind the mirror.
For instance, rays emanating from the tip ![]() of the object
appear, after reflection from the
mirror, to come from a point
of the object
appear, after reflection from the
mirror, to come from a point ![]() which is behind the
mirror. Note that only two rays are used to locate
which is behind the
mirror. Note that only two rays are used to locate ![]() , for
the sake of clarity. In fact, two is the minimum number of rays
needed to locate a point image.
Of course,
the image behind the mirror
cannot be viewed by projecting it onto a screen, because
there are no real light-rays behind the mirror. This
type of image is termed a virtual image. The characteristic
difference
between a real image and a virtual image is that, immediately after
reflection from the mirror, light-rays emitted by the object converge
on a real image, but diverge from a virtual image.
According to Fig. 72, the image is upright with
respect to the object, and is also magnified.
, for
the sake of clarity. In fact, two is the minimum number of rays
needed to locate a point image.
Of course,
the image behind the mirror
cannot be viewed by projecting it onto a screen, because
there are no real light-rays behind the mirror. This
type of image is termed a virtual image. The characteristic
difference
between a real image and a virtual image is that, immediately after
reflection from the mirror, light-rays emitted by the object converge
on a real image, but diverge from a virtual image.
According to Fig. 72, the image is upright with
respect to the object, and is also magnified.
The graphical method described above is fine for developing an intuitive understanding of image formation by concave mirrors, or for checking a calculation, but is a bit too cumbersome for everyday use. The analytic method described below is far more flexible.
Consider an object ![]() placed a distance
placed a distance ![]() in front of
a concave mirror of radius of curvature
in front of
a concave mirror of radius of curvature ![]() . In order to find
the image
. In order to find
the image ![]() produced by the mirror, we draw two rays from
produced by the mirror, we draw two rays from
![]() to the mirror--see Fig. 73. The first, labelled 1, travels from
to the mirror--see Fig. 73. The first, labelled 1, travels from ![]() to the
vertex
to the
vertex ![]() and is reflected such that its angle of
incidence
and is reflected such that its angle of
incidence ![]() equals its angle of reflection. The second
ray, labelled 2, passes through the centre of curvature
equals its angle of reflection. The second
ray, labelled 2, passes through the centre of curvature ![]() of
the mirror, strikes the mirror at point
of
the mirror, strikes the mirror at point ![]() , and is reflected
back along its own path. The two rays meet at point
, and is reflected
back along its own path. The two rays meet at point ![]() .
Thus,
.
Thus, ![]() is the image of
is the image of ![]() , since point
, since point ![]() must lie on the
principal axis.
must lie on the
principal axis.
In the triangle ![]() , we have
, we have
![]() , and in the
triangle
, and in the
triangle ![]() we have
we have
![]() , where
, where ![]() is
the object distance, and
is
the object distance, and ![]() is the image distance. Here,
is the image distance. Here,
![]() is the height of the object, and
is the height of the object, and ![]() is the height of
the image. By convention,
is the height of
the image. By convention, ![]() is a negative number, since
the image is inverted (if the image were upright then
is a negative number, since
the image is inverted (if the image were upright then ![]() would be a positive number). It follows that
would be a positive number). It follows that
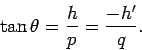 |
(351) |
From triangles ![]() and
and ![]() , we have
, we have
![]() and
and
![]() , respectively.
These expressions yield
, respectively.
These expressions yield
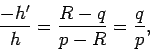 |
(354) |
For an object which is very far away from
the mirror (i.e.,
![]() ),
so that light-rays from the object are parallel to the principal
axis, we expect the image to form at the focal point
),
so that light-rays from the object are parallel to the principal
axis, we expect the image to form at the focal point
![]() of the mirror. Thus, in this case,
of the mirror. Thus, in this case, ![]() , where
, where ![]() is
the focal length of the mirror, and Eq. (355) reduces to
is
the focal length of the mirror, and Eq. (355) reduces to
| (356) |
The above expression was derived for the case of a real
image. However, as is easily demonstrated, it also applies
to virtual images provided that the following sign convention
is adopted. For real images, which always form in front
of the mirror, the image distance ![]() is positive. For
virtual images, which always form behind the mirror,
the image distance
is positive. For
virtual images, which always form behind the mirror,
the image distance ![]() is negative. It immediately follows,
from Eq. (352), that real images are always inverted, and
virtual images are always upright. Table 5
shows how the location and character of the image formed
in a concave spherical mirror depend on the location of
the object, according to Eqs. (352) and (358). It is
clear that the modus operandi of a shaving mirror,
or a makeup mirror, is to place the object (i.e., a
face) between the mirror and the focus of the mirror. The image
is upright, (apparently) located behind the mirror, and magnified.
is negative. It immediately follows,
from Eq. (352), that real images are always inverted, and
virtual images are always upright. Table 5
shows how the location and character of the image formed
in a concave spherical mirror depend on the location of
the object, according to Eqs. (352) and (358). It is
clear that the modus operandi of a shaving mirror,
or a makeup mirror, is to place the object (i.e., a
face) between the mirror and the focus of the mirror. The image
is upright, (apparently) located behind the mirror, and magnified.