Next: Electromagnetic Waves in Conductors Up: Dispersive Waves Previous: Parallel EM Waves in Contents
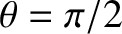 , the eigenmode equation
(9.168) simplifies to
One obvious way of solving this equation is to have
, the eigenmode equation
(9.168) simplifies to
One obvious way of solving this equation is to have
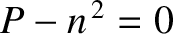 , or
with the eigenvector
, or
with the eigenvector
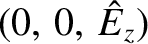 . Because the wavevector now points in the
. Because the wavevector now points in the
 -direction, this is clearly a transverse wave polarized with its electric
field parallel to the equilibrium magnetic field. Particle motions are
along the magnetic field, so the mode dynamics are completely unaffected
by this field. Thus, the wave is identical to the
electromagnetic plasma wave found
previously in an unmagnetized plasma. (See Section 9.3.) This wave is known as the ordinary,
or
-direction, this is clearly a transverse wave polarized with its electric
field parallel to the equilibrium magnetic field. Particle motions are
along the magnetic field, so the mode dynamics are completely unaffected
by this field. Thus, the wave is identical to the
electromagnetic plasma wave found
previously in an unmagnetized plasma. (See Section 9.3.) This wave is known as the ordinary,
or  -, mode.
-, mode.
The other solution to Equation (9.192) is obtained by setting the 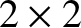 determinant
involving the
determinant
involving the  - and
- and  -components of the electric field to zero. With the help of
the identity
-components of the electric field to zero. With the help of
the identity
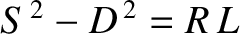 , the
dispersion relation reduces to
, the
dispersion relation reduces to
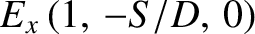 .
.
Let us, first of all, search for the cutoff frequencies, at which  goes to
zero.
According to Equation (9.194), these frequencies are the roots of
goes to
zero.
According to Equation (9.194), these frequencies are the roots of  and
and  .
In fact, we have already solved these equations;
there are two cutoff frequencies,
.
In fact, we have already solved these equations;
there are two cutoff frequencies,  and
and 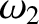 ,
that are specified by Equations (9.188) and (9.191), respectively.
,
that are specified by Equations (9.188) and (9.191), respectively.
Let us, next, search for the resonant frequencies, at which  goes to
infinity. According to Equation (9.194), the
resonant frequencies are solutions of
goes to
infinity. According to Equation (9.194), the
resonant frequencies are solutions of
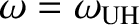 ,
where
,
where
 |
(9.196) |
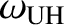 is a good approximation
of one of the roots of Equation (9.195). To
obtain the second root, we make use of the fact that the product of the square
of the roots
is
is a good approximation
of one of the roots of Equation (9.195). To
obtain the second root, we make use of the fact that the product of the square
of the roots
is
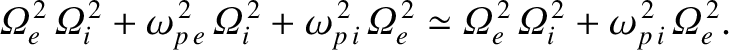 |
(9.197) |
 , where
, where
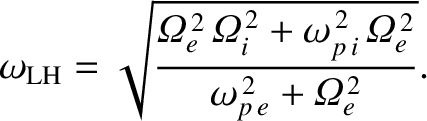 |
(9.198) |
The first resonant frequency,
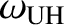 , is greater than the
electron cyclotron or plasma frequencies, and is called the upper hybrid
frequency. The second resonant frequency,
, is greater than the
electron cyclotron or plasma frequencies, and is called the upper hybrid
frequency. The second resonant frequency,
 , lies between the
electron and ion cyclotron frequencies, and is called the
lower hybrid frequency.
Unfortunately, there is no simple explanation of the origins of the
two hybrid resonances in terms of the motions of individual particles.
At low frequencies, the mode in question
reverts to the compressional-Alfvén wave
discussed previously. Note that the shear-Alfvén wave does not
propagate perpendicular to the magnetic field.
, lies between the
electron and ion cyclotron frequencies, and is called the
lower hybrid frequency.
Unfortunately, there is no simple explanation of the origins of the
two hybrid resonances in terms of the motions of individual particles.
At low frequencies, the mode in question
reverts to the compressional-Alfvén wave
discussed previously. Note that the shear-Alfvén wave does not
propagate perpendicular to the magnetic field.
![\includegraphics[width=0.7\textwidth]{Chapter09/fig9_04.eps}](img2888.png) |
Using the previous information, and the easily demonstrated fact that
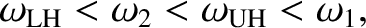 |
(9.199) |
 -, mode.
The upper branch is basically a linearly polarized (in the
-, mode.
The upper branch is basically a linearly polarized (in the  -direction)
electromagnetic wave, somewhat modified by the presence of the plasma. This
branch corresponds to a wave that
propagates in the absence of an equilibrium magnetic field. The lowest
branch corresponds to a wave that does not propagate in the absence of an
equilibrium field. Finally, the middle branch corresponds to a wave that
converts into an electrostatic plasma wave in the absence of an equilibrium
magnetic field.
-direction)
electromagnetic wave, somewhat modified by the presence of the plasma. This
branch corresponds to a wave that
propagates in the absence of an equilibrium magnetic field. The lowest
branch corresponds to a wave that does not propagate in the absence of an
equilibrium field. Finally, the middle branch corresponds to a wave that
converts into an electrostatic plasma wave in the absence of an equilibrium
magnetic field.
Wave propagation at oblique angles is generally more complicated than propagation parallel or perpendicular to the equilibrium magnetic field, but does not involve any new physical effects (Stix 1992; Swanson 2003).