Next: Compound Pendulum Up: Simple Harmonic Oscillation Previous: LC Circuit Contents
Consider a compact mass  suspended from a light inextensible string of length
suspended from a light inextensible string of length  , such that the
mass is free to swing from side to side in a vertical plane, as shown in
Figure 1.8.
This setup is known as a simple pendulum.
Let
, such that the
mass is free to swing from side to side in a vertical plane, as shown in
Figure 1.8.
This setup is known as a simple pendulum.
Let 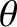 be the angle subtended between the string and
the downward vertical. The stable equilibrium state of the system corresponds to
the situation in which the mass is stationary, and hangs vertically down (
i.e.,
be the angle subtended between the string and
the downward vertical. The stable equilibrium state of the system corresponds to
the situation in which the mass is stationary, and hangs vertically down (
i.e.,
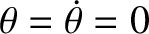 ).
The angular equation of motion of the pendulum is (Fowles and Cassiday 2005)
).
The angular equation of motion of the pendulum is (Fowles and Cassiday 2005)
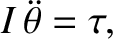 |
(1.48) |
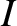 is the moment of inertia of the mass, and
is the moment of inertia of the mass, and 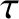 the torque acting
about the suspension point.
For the
case in hand, given that the mass is essentially a point particle, and is situated a distance
the torque acting
about the suspension point.
For the
case in hand, given that the mass is essentially a point particle, and is situated a distance  from
the axis of rotation (i.e., from the suspension point), it follows that
from
the axis of rotation (i.e., from the suspension point), it follows that
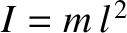 (ibid.).
(ibid.).
The two forces acting on the mass are the downward gravitational force, 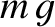 , where
, where 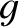 is the acceleration due to gravity,
and the tension,
is the acceleration due to gravity,
and the tension,  , in the string.
However, the tension makes no contribution to the torque,
because its line of action passes
through the suspension point. From elementary trigonometry,
the line of action of the gravitational force passes a perpendicular distance
, in the string.
However, the tension makes no contribution to the torque,
because its line of action passes
through the suspension point. From elementary trigonometry,
the line of action of the gravitational force passes a perpendicular distance
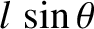 from the
suspension point. Hence, the magnitude of the gravitational torque is
from the
suspension point. Hence, the magnitude of the gravitational torque is
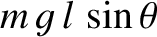 .
Moreover, the gravitational torque is a restoring torque; that is, if
the mass is
displaced slightly from its equilibrium position (i.e.,
.
Moreover, the gravitational torque is a restoring torque; that is, if
the mass is
displaced slightly from its equilibrium position (i.e., 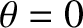 ) then the
gravitational torque acts
to push the mass back toward that position. Thus, we can write
) then the
gravitational torque acts
to push the mass back toward that position. Thus, we can write
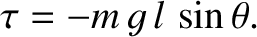 |
(1.49) |
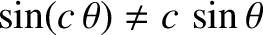 , where
, where 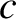 is an arbitrary constant], which means that it is generally
very difficult to solve.
is an arbitrary constant], which means that it is generally
very difficult to solve.
Suppose, however, that the system does not stray very far from
its equilibrium position (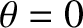 ). If this is the case then we
can expand
). If this is the case then we
can expand
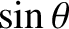 in a Taylor series about
in a Taylor series about 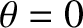 . (See Appendix B.) We obtain
. (See Appendix B.) We obtain
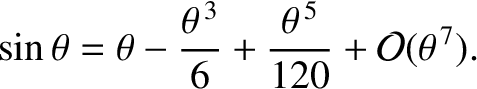 |
(1.51) |
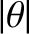 is sufficiently small then the series is dominated by its
first term, and we can write
is sufficiently small then the series is dominated by its
first term, and we can write
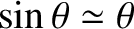 . This is known
as the small-angle approximation.
Making use of this approximation,
the equation of motion (1.50) simplifies to
where
. This is known
as the small-angle approximation.
Making use of this approximation,
the equation of motion (1.50) simplifies to
where
 |
(1.53) |
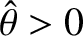 and
and  are constants.
We conclude that the pendulum swings back and forth at a fixed angular frequency,
are constants.
We conclude that the pendulum swings back and forth at a fixed angular frequency,  , that depends on
, that depends on  and
and 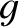 , but is independent of the amplitude,
, but is independent of the amplitude,
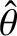 , of the motion. This result only holds as long as
the small-angle approximation remains valid. It turns out that
, of the motion. This result only holds as long as
the small-angle approximation remains valid. It turns out that
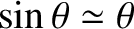 is a reasonably good approximation provided
is a reasonably good approximation provided
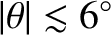 . Hence, the period
of a simple pendulum is only amplitude independent when the (angular) amplitude of its motion
is less than about
. Hence, the period
of a simple pendulum is only amplitude independent when the (angular) amplitude of its motion
is less than about  .
.