Next: Oscillation of an Elastic Up: Multi-Dimensional Waves Previous: Cylindrical Waves Contents
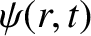 , where
, where
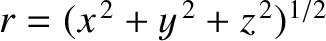 is a standard radial
spherical coordinate (Fitzpatrick 2008). Assuming that this function satisfies the three-dimensional wave equation, (7.9), which
can be rewritten (see Exercise 3)
it can be shown (see Exercise 3) that a sinusoidal spherical wave of phase angle
is a standard radial
spherical coordinate (Fitzpatrick 2008). Assuming that this function satisfies the three-dimensional wave equation, (7.9), which
can be rewritten (see Exercise 3)
it can be shown (see Exercise 3) that a sinusoidal spherical wave of phase angle  , wavenumber
, wavenumber  , and angular frequency
, and angular frequency
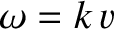 , has the
wavefunction
Here,
, has the
wavefunction
Here,  is the amplitude of the wave.
The associated wavefronts are a set of concentric spheres that
propagate radially outward, from their common center (
is the amplitude of the wave.
The associated wavefronts are a set of concentric spheres that
propagate radially outward, from their common center (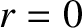 ), at the phase velocity
), at the phase velocity
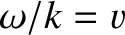 . The wave amplitude attenuates as
. The wave amplitude attenuates as 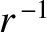 .
Such behavior can again be understood as a consequence of energy conservation, according to which the power flowing across the various
.
Such behavior can again be understood as a consequence of energy conservation, according to which the power flowing across the various
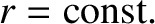 surfaces must be
constant. (The area of a constant-
surfaces must be
constant. (The area of a constant-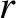 surface scales as
surface scales as
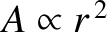 ,
and the power flowing across such a surface is proportional to
,
and the power flowing across such a surface is proportional to
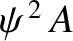 .)
The spherical wave specified in expression (7.13) is such as would be generated by
a point source located at
.)
The spherical wave specified in expression (7.13) is such as would be generated by
a point source located at 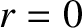 .
.