Wave Propagation in Inhomogeneous Media
We saw in Section 6.7 that if a wave is normally incident at an interface between two media of substantially different impedances then
a significant fraction of the wave energy is reflected. Moreover, this reflection takes place in such a manner that the net energy flux on either side of the interface
is the same. On the other hand, if the two media have similar impedances then the reflected energy fraction is small. In this case, the
incident and transmitted waves have the same frequency (because this property of the waves is determined by the source) but
slightly different wavenumbers (assuming that the characteristic wave propagation speeds on either side of the interface are
slightly different).
Suppose that a wave
travels though a medium whose impedance and characteristic wave propagation speed are slowly-varying functions of position. We would expect such a wave to propagate
through the medium without significant reflection. Moreover, the frequency of the wave should remain fixed, while its wavenumber
slowly varies with position, in accordance with the dispersion relation. Finally, the amplitude of the wave should vary
slowly with position in such a manner that the energy flux remains constant. Let us investigate further.
Suppose that the medium has a characteristic wave propagation speed 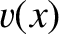 , and a wave impedance
, and a wave impedance 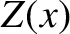 . The local wave dispersion
relation is assumed to take the form
. The local wave dispersion
relation is assumed to take the form
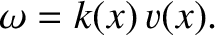 |
(6.162) |
Hence, at fixed wave frequency, the wavenumber varies with position as
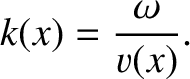 |
(6.163) |
If 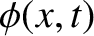 is the phase of the wave then the most general definitions of angular frequency and wavenumber are
respectively. (See Section 9.11.)
It follows that, in the present case,
is the phase of the wave then the most general definitions of angular frequency and wavenumber are
respectively. (See Section 9.11.)
It follows that, in the present case,
![$\displaystyle \phi(x,t) = \omega\left(t-\int^x\left[v(x')\right]^{-1}\,dx'\right).$](img1728.png) |
(6.166) |
Hence, the wavefunction can be written
![$\displaystyle \psi(x,t) = A(x)\,\cos[\phi(x,t)]= A(x)\,\cos\left[ \omega\left(t-\int^x\left[v(x')\right]^{-1}\,dx'\right)\right],$](img1729.png) |
(6.167) |
where 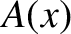 is the wave amplitude. The mean energy flux associated with the wave is
is the wave amplitude. The mean energy flux associated with the wave is
![$\displaystyle \langle {\cal I}\rangle = \frac{1}{2}\,\omega^{\,2}\,Z(x)\left[A(x)\right]^{\,2}.$](img1731.png) |
(6.168) |
(See Section 6.5.)
We would expect this flux to be position independent (otherwise, energy would not be conserved), which implies that
![$A(x)\propto [Z(x)]^{-1/2}$](img1732.png) . Thus, we obtain
. Thus, we obtain
![$\displaystyle \psi(x,t) = \frac{A_0}{[Z(x)]^{1/2}}\,\cos\left[ \omega\left(t-\int^x\left[v(x')\right]^{-1}\,dx'\right)\right],$](img1733.png) |
(6.169) |
where 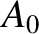 is a constant. The previous expression, which is known as the WKB solution (WKB stands for Wentzel–Kramers–Brillouin),
is not exact. However, it can be demonstrated that the WKB solution is a good approximation to the true solution of the inhomogeneous wave equation in the limit that the variations in
is a constant. The previous expression, which is known as the WKB solution (WKB stands for Wentzel–Kramers–Brillouin),
is not exact. However, it can be demonstrated that the WKB solution is a good approximation to the true solution of the inhomogeneous wave equation in the limit that the variations in 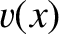 and
and 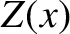 take place on lengthscales that are much longer than the
wavelength of the wave (Schiff 1955). On the other hand, the WKB solution breaks down completely if the variations in
take place on lengthscales that are much longer than the
wavelength of the wave (Schiff 1955). On the other hand, the WKB solution breaks down completely if the variations in 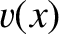 and
and 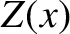 take place on lengthscales smaller than, or similar to, the wavelength.
take place on lengthscales smaller than, or similar to, the wavelength.
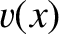 , and a wave impedance
, and a wave impedance 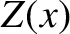 . The local wave dispersion
relation is assumed to take the form
. The local wave dispersion
relation is assumed to take the form
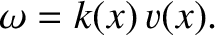
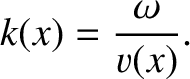
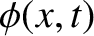 is the phase of the wave then the most general definitions of angular frequency and wavenumber are
is the phase of the wave then the most general definitions of angular frequency and wavenumber are
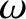
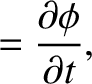
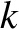
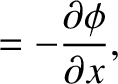
![$\displaystyle \phi(x,t) = \omega\left(t-\int^x\left[v(x')\right]^{-1}\,dx'\right).$](img1728.png)
![$\displaystyle \psi(x,t) = A(x)\,\cos[\phi(x,t)]= A(x)\,\cos\left[ \omega\left(t-\int^x\left[v(x')\right]^{-1}\,dx'\right)\right],$](img1729.png)
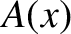 is the wave amplitude. The mean energy flux associated with the wave is
is the wave amplitude. The mean energy flux associated with the wave is
![$\displaystyle \langle {\cal I}\rangle = \frac{1}{2}\,\omega^{\,2}\,Z(x)\left[A(x)\right]^{\,2}.$](img1731.png)
![$A(x)\propto [Z(x)]^{-1/2}$](img1732.png) . Thus, we obtain
. Thus, we obtain
![$\displaystyle \psi(x,t) = \frac{A_0}{[Z(x)]^{1/2}}\,\cos\left[ \omega\left(t-\int^x\left[v(x')\right]^{-1}\,dx'\right)\right],$](img1733.png)
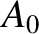 is a constant. The previous expression, which is known as the WKB solution (WKB stands for Wentzel–Kramers–Brillouin),
is not exact. However, it can be demonstrated that the WKB solution is a good approximation to the true solution of the inhomogeneous wave equation in the limit that the variations in
is a constant. The previous expression, which is known as the WKB solution (WKB stands for Wentzel–Kramers–Brillouin),
is not exact. However, it can be demonstrated that the WKB solution is a good approximation to the true solution of the inhomogeneous wave equation in the limit that the variations in 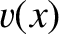 and
and 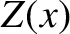 take place on lengthscales that are much longer than the
wavelength of the wave (Schiff 1955). On the other hand, the WKB solution breaks down completely if the variations in
take place on lengthscales that are much longer than the
wavelength of the wave (Schiff 1955). On the other hand, the WKB solution breaks down completely if the variations in 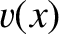 and
and 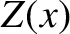 take place on lengthscales smaller than, or similar to, the wavelength.
take place on lengthscales smaller than, or similar to, the wavelength.