Wave Interference
What is the relationship between traveling wave and standing
wave solutions to the wave equation, (6.1), in an infinite medium? To help answer this question, let us form a superposition of two traveling wave solutions
of equal amplitude 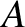 , and zero phase angle
, and zero phase angle  , that have the same wavenumber
, that have the same wavenumber
 , but are moving in opposite directions. In other words,
, but are moving in opposite directions. In other words,
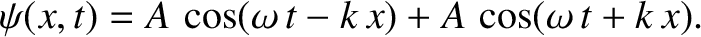 |
(6.19) |
Because the wave equation, (6.1), is linear, the previous superposition is a valid solution
provided the two component waves are also valid solutions; that is, provided
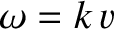 , which we shall assume to be the case. Making
use of the trigonometric identity
, which we shall assume to be the case. Making
use of the trigonometric identity
![$\cos a + \cos b\equiv 2\,\cos[(a+b)/2]\,\cos[(a-b)/2]$](img723.png) (see Appendix B),
the previous expression can also be written
(see Appendix B),
the previous expression can also be written
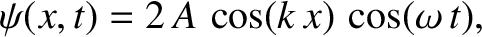 |
(6.20) |
which is a standing wave [cf., Equation (6.2)]. Evidently, a standing wave is a linear
superposition of two, otherwise identical, traveling waves that propagate in opposite
directions. The two waves completely cancel one another out at the nodes, which
are situated at
 , where
, where  is an integer. This process is known as total
destructive interference. On the other hand, the waves reinforce one another
at the anti-nodes, which are situated at
is an integer. This process is known as total
destructive interference. On the other hand, the waves reinforce one another
at the anti-nodes, which are situated at
 , generating a wave
whose amplitude is twice that of the component waves. This process
is known as constructive interference.
, generating a wave
whose amplitude is twice that of the component waves. This process
is known as constructive interference.
As a more general example of wave interference, consider a superposition
of two traveling waves of unequal amplitudes which again have the same wavenumber
and zero phase angle,
and are moving in opposite directions; that is,
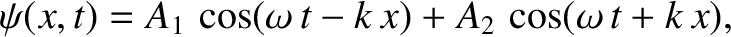 |
(6.21) |
where
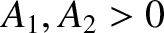 .
In this case, the trigonometric identities
.
In this case, the trigonometric identities
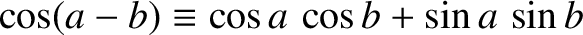 and
and
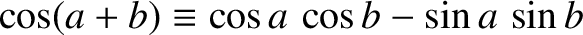 (see Appendix B) yield
(see Appendix B) yield
 |
(6.22) |
Thus, the two waves interfere destructively at
 [i.e., at points where
[i.e., at points where
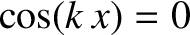 and
and
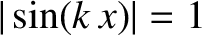 ] to produce a minimum wave amplitude
] to produce a minimum wave amplitude 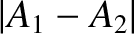 , and interfere constructively
at
, and interfere constructively
at
 [i.e., at points where
[i.e., at points where
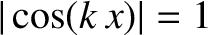 and
and
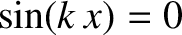 ] to produce a maximum wave amplitude
] to produce a maximum wave amplitude 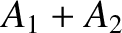 . It can
be seen
that the destructive interference is incomplete unless
. It can
be seen
that the destructive interference is incomplete unless 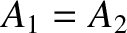 . Incidentally, it is a general
result that if two waves of amplitude
. Incidentally, it is a general
result that if two waves of amplitude 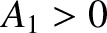 and
and  interfere then
the maximum and minimum possible values of the resulting wave amplitude are
interfere then
the maximum and minimum possible values of the resulting wave amplitude are 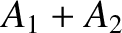 and
and
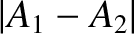 , respectively.
, respectively.
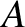 , and zero phase angle
, and zero phase angle  , that have the same wavenumber
, that have the same wavenumber
 , but are moving in opposite directions. In other words,
, but are moving in opposite directions. In other words,
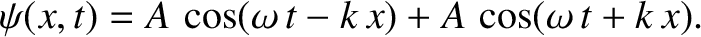
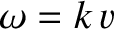 , which we shall assume to be the case. Making
use of the trigonometric identity
, which we shall assume to be the case. Making
use of the trigonometric identity
![$\cos a + \cos b\equiv 2\,\cos[(a+b)/2]\,\cos[(a-b)/2]$](img723.png) (see Appendix B),
the previous expression can also be written
(see Appendix B),
the previous expression can also be written
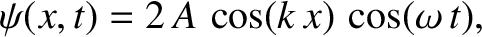
 , where
, where  is an integer. This process is known as total
destructive interference. On the other hand, the waves reinforce one another
at the anti-nodes, which are situated at
is an integer. This process is known as total
destructive interference. On the other hand, the waves reinforce one another
at the anti-nodes, which are situated at
 , generating a wave
whose amplitude is twice that of the component waves. This process
is known as constructive interference.
, generating a wave
whose amplitude is twice that of the component waves. This process
is known as constructive interference.
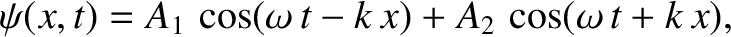
 .
In this case, the trigonometric identities
.
In this case, the trigonometric identities
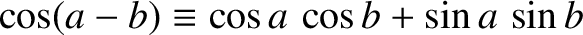 and
and
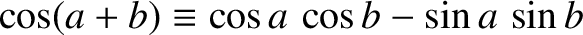 (see Appendix B) yield
(see Appendix B) yield

 [i.e., at points where
[i.e., at points where
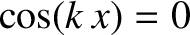 and
and
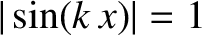 ] to produce a minimum wave amplitude
] to produce a minimum wave amplitude 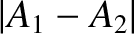 , and interfere constructively
at
, and interfere constructively
at
 [i.e., at points where
[i.e., at points where
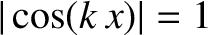 and
and
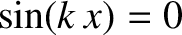 ] to produce a maximum wave amplitude
] to produce a maximum wave amplitude 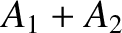 . It can
be seen
that the destructive interference is incomplete unless
. It can
be seen
that the destructive interference is incomplete unless 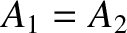 . Incidentally, it is a general
result that if two waves of amplitude
. Incidentally, it is a general
result that if two waves of amplitude 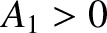 and
and  interfere then
the maximum and minimum possible values of the resulting wave amplitude are
interfere then
the maximum and minimum possible values of the resulting wave amplitude are 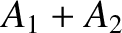 and
and
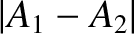 , respectively.
, respectively.