Next: Two Coupled LC Circuits Up: Coupled Oscillations Previous: Introduction Contents
 that are free to slide over a frictionless horizontal surface. Suppose that
the masses are attached to one another, and to two immovable
walls, by means of three identical light horizontal springs of spring constant
that are free to slide over a frictionless horizontal surface. Suppose that
the masses are attached to one another, and to two immovable
walls, by means of three identical light horizontal springs of spring constant  , as
shown in Figure 3.1. The instantaneous state of the system
is conveniently specified by the displacements of the left and
right masses,
, as
shown in Figure 3.1. The instantaneous state of the system
is conveniently specified by the displacements of the left and
right masses, 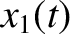 and
and 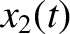 , respectively. The extensions
of the left, middle, and right springs are
, respectively. The extensions
of the left, middle, and right springs are  ,
, 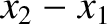 , and
, and 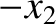 ,
respectively, assuming that
,
respectively, assuming that 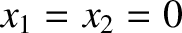 corresponds to the equilibrium configuration in which the springs are all
unextended. The equations of motion of the two masses
are thus
Here, we have made use of the fact that a mass attached to the left end of a
spring of extension
corresponds to the equilibrium configuration in which the springs are all
unextended. The equations of motion of the two masses
are thus
Here, we have made use of the fact that a mass attached to the left end of a
spring of extension  and spring constant
and spring constant  experiences a horizontal force
experiences a horizontal force 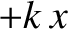 ,
whereas a mass attached to the right end of the same spring experiences an
equal and opposite force
,
whereas a mass attached to the right end of the same spring experiences an
equal and opposite force 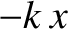 .
.
Equations (3.1)–(3.2) can be rewritten in the form
where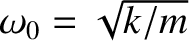 . Let us search for a solution in which the two
masses oscillate in phase with one another at the same angular frequency,
. Let us search for a solution in which the two
masses oscillate in phase with one another at the same angular frequency,  . In other words,
where
. In other words,
where 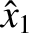 ,
, 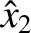 , and
, and  are constants. Equations (3.3) and
(3.4) yield
are constants. Equations (3.3) and
(3.4) yield
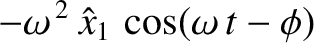 |
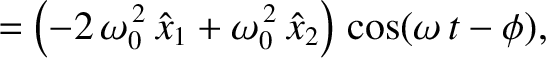 |
(3.7) |
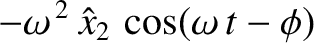 |
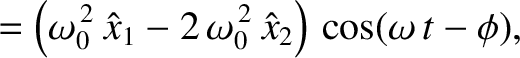 |
(3.8) |
 , dividing through by
, dividing through by  , and rearranging),
where
, and rearranging),
where
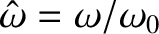 . Note that, by searching for a solution
of the form (3.5)–(3.6), we have effectively converted the system of two coupled
linear differential equations (3.3)–(3.4) into the much simpler system of two coupled linear algebraic
equations (3.9)–(3.10). The latter equations have the trivial solutions
. Note that, by searching for a solution
of the form (3.5)–(3.6), we have effectively converted the system of two coupled
linear differential equations (3.3)–(3.4) into the much simpler system of two coupled linear algebraic
equations (3.9)–(3.10). The latter equations have the trivial solutions
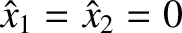 , but also yield
Hence, the condition for a nontrivial solution is
In fact, if we write Equations (3.9)–(3.10) in the form of a homogenous (i.e., with a null right-hand side)
, but also yield
Hence, the condition for a nontrivial solution is
In fact, if we write Equations (3.9)–(3.10) in the form of a homogenous (i.e., with a null right-hand side) 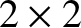 matrix equation, so that
matrix equation, so that
![\begin{displaymath}\left(
\begin{array}{cc}
\hat{\omega}^{\,2}-2, & 1\\ [0.5ex]
...
...t) = \left(
\begin{array}{c}
0\\ [0.5ex] 0
\end{array}\right) ,\end{displaymath}](img687.png) |
(3.13) |
Equation (3.12) can be rewritten
It follows that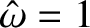 or or 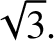 |
(3.15) |
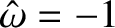 and
and
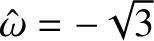 —because a negative frequency oscillation
is equivalent to an oscillation with an equal and opposite positive frequency, and
an equal and opposite phase. In other words,
—because a negative frequency oscillation
is equivalent to an oscillation with an equal and opposite positive frequency, and
an equal and opposite phase. In other words,
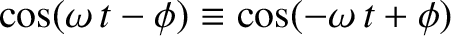 .
It is thus apparent that
the dynamical system pictured in Figure 3.1 has two unique frequencies of oscillation: namely,
.
It is thus apparent that
the dynamical system pictured in Figure 3.1 has two unique frequencies of oscillation: namely,
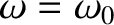 and
and
 . These are called the normal frequencies of the
system.
Because the system possesses two degrees of
freedom (i.e., two independent coordinates are needed to specify its
instantaneous configuration), it is not entirely surprising that it possesses two
normal frequencies. In fact, it is a general rule that a dynamical system
with
. These are called the normal frequencies of the
system.
Because the system possesses two degrees of
freedom (i.e., two independent coordinates are needed to specify its
instantaneous configuration), it is not entirely surprising that it possesses two
normal frequencies. In fact, it is a general rule that a dynamical system
with  degrees of freedom possesses
degrees of freedom possesses  normal frequencies.
normal frequencies.
The patterns of motion associated with the two normal frequencies
can be deduced from Equation (3.11). Thus, for
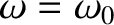 (i.e.,
(i.e.,
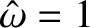 ), we
get
), we
get
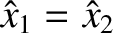 , so that
, so that
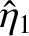 and
and 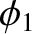 are arbitrary constants. This first pattern of motion corresponds to the two masses
executing simple harmonic oscillation with the same amplitude and phase.
Such an oscillation does not stretch the middle spring.
On the other hand, for
are arbitrary constants. This first pattern of motion corresponds to the two masses
executing simple harmonic oscillation with the same amplitude and phase.
Such an oscillation does not stretch the middle spring.
On the other hand, for
 (i.e.,
(i.e.,
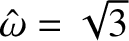 ), we get
), we get
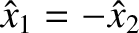 , so that
where
, so that
where
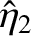 and
and 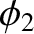 are arbitrary constants. This second pattern of motion
corresponds to the two masses executing simple harmonic oscillation with the
same amplitude but in anti-phase; that is, with a phase shift of
are arbitrary constants. This second pattern of motion
corresponds to the two masses executing simple harmonic oscillation with the
same amplitude but in anti-phase; that is, with a phase shift of 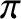 radians. Such oscillations do stretch the
middle spring, implying that the restoring force associated with
similar amplitude displacements is greater for the second
pattern of motion than for the first. This accounts for the higher
oscillation frequency in the second case. (The inertia is the same in both cases, so the
oscillation frequency is proportional to the square root of the restoring force
associated with similar amplitude displacements.) The two distinctive
patterns of motion that we have found are called the normal modes of
oscillation of the system. Incidentally, it is a general rule that a dynamical system
possessing
radians. Such oscillations do stretch the
middle spring, implying that the restoring force associated with
similar amplitude displacements is greater for the second
pattern of motion than for the first. This accounts for the higher
oscillation frequency in the second case. (The inertia is the same in both cases, so the
oscillation frequency is proportional to the square root of the restoring force
associated with similar amplitude displacements.) The two distinctive
patterns of motion that we have found are called the normal modes of
oscillation of the system. Incidentally, it is a general rule that a dynamical system
possessing  degrees of freedom has
degrees of freedom has  unique normal modes of oscillation.
unique normal modes of oscillation.
The most general motion of the system is a
linear combination of the two normal modes. This immediately follows because
Equations (3.1) and (3.2) are linear equations. [In other
words, if 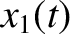 and
and 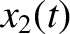 are solutions then so are
are solutions then so are
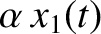 and
and
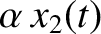 ,
where
,
where 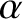 is an arbitrary constant.] Thus, we can write
is an arbitrary constant.] Thus, we can write
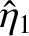 ,
, 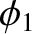 ,
,
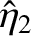 , and
, and 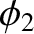 . (In general,
we expect the solution of a second-order ordinary differential equation to
contain two arbitrary constants. It, thus, follows that the solution of a system of two
coupled, second-order, ordinary differential equations should contain four arbitrary constants.)
These constants are determined by the initial conditions.
. (In general,
we expect the solution of a second-order ordinary differential equation to
contain two arbitrary constants. It, thus, follows that the solution of a system of two
coupled, second-order, ordinary differential equations should contain four arbitrary constants.)
These constants are determined by the initial conditions.
For instance, suppose that 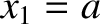 ,
,
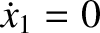 ,
, 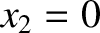 , and
, and
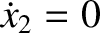 at
at  . It follows, from Equations (3.20) and (3.21), that
. It follows, from Equations (3.20) and (3.21), that
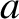 |
 |
(3.22) |
| 0 | 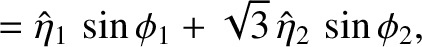 |
(3.23) |
| 0 | 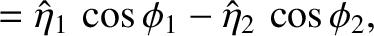 |
(3.24) |
| 0 | 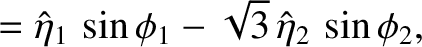 |
(3.25) |
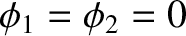 and
and
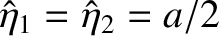 . Thus, the
system evolves in time as
. Thus, the
system evolves in time as
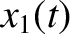 |
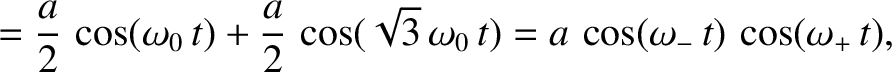 |
(3.26) |
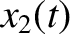 |
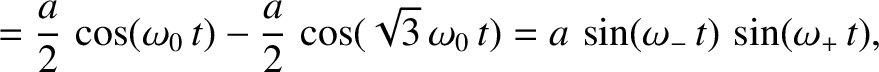 |
(3.27) |
![$\omega_\pm = [(\sqrt{3}\pm 1)/2]]\,\omega_0$](img722.png) , and
use has been made of the trigonometric identities
, and
use has been made of the trigonometric identities
![$\cos a + \cos b\equiv 2\,\cos[(a+b)/2]\,\cos[(a-b)/2]$](img723.png) and
and
![$\cos a - \cos b \equiv -2\,\sin[(a+b)/2]\,\sin[(a-b)/2]$](img620.png) . (See Appendix B.) This evolution is
illustrated in Figure 3.2.
. (See Appendix B.) This evolution is
illustrated in Figure 3.2.
![\includegraphics[width=0.8\textwidth]{Chapter03/fig3_02.eps}](img724.png) |
Finally, let us define the so-called normal coordinates, which (in the present case) take the form
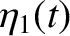 |
![$\displaystyle = [x_1(t) + x_2(t)]/2,$](img727.png) |
(3.28) |
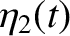 |
![$\displaystyle = [x_1(t)-x_2(t)]/2.$](img729.png) |
(3.29) |
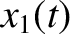 and
and 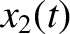 . See Figures 3.2 and 3.3.
This suggests that the equations of motion of the system should look particularly simple when expressed in terms of the normal coordinates. In fact, it
can be seen that the
sum of Equations (3.3) and (3.4) reduces to
whereas the difference gives
Thus, when expressed in terms of the normal coordinates, the equations of motion
of the system reduce to two uncoupled simple harmonic oscillator
equations.
The most general solution to Equation (3.32) is (3.30),
whereas the most general solution to Equation (3.33) is (3.31).
Hence, if we can guess the normal coordinates of a coupled oscillatory
system then the determination of the normal modes of oscillation is considerably simplified.
. See Figures 3.2 and 3.3.
This suggests that the equations of motion of the system should look particularly simple when expressed in terms of the normal coordinates. In fact, it
can be seen that the
sum of Equations (3.3) and (3.4) reduces to
whereas the difference gives
Thus, when expressed in terms of the normal coordinates, the equations of motion
of the system reduce to two uncoupled simple harmonic oscillator
equations.
The most general solution to Equation (3.32) is (3.30),
whereas the most general solution to Equation (3.33) is (3.31).
Hence, if we can guess the normal coordinates of a coupled oscillatory
system then the determination of the normal modes of oscillation is considerably simplified.
Note that, in general, the normal coordinates of a multiple-degree-of-freedom oscillatory system are linear combinations of the physical coordinates. By definition, the equations of motion of the system become decoupled from one another when expressed in terms of the normal coordinates. In fact, each equation of motion takes the form of a simple harmonic oscillator equation whose characteristic frequency is one of the normal frequencies. Consequently, each normal coordinate executes simple harmonic oscillation at its associated normal frequency.
![\includegraphics[width=0.8\textwidth]{Chapter03/fig3_03.eps}](img734.png) |