Next: Coupled Oscillations Up: Damped and Driven Harmonic Previous: Transient Oscillator Response Contents
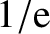 of its initial
value after
of its initial
value after 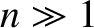 periods show that the ratio of the period of oscillation to the period
of the oscillation with no damping is approximately
periods show that the ratio of the period of oscillation to the period
of the oscillation with no damping is approximately
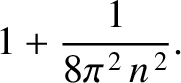
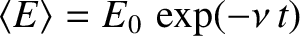 .
It is possible to define an effective quality factor for such oscillators as
.
It is possible to define an effective quality factor for such oscillators as
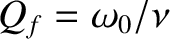 , where
, where
 is the natural angular oscillation frequency.
is the natural angular oscillation frequency.
For example, when the note “middle C” on
a piano is struck its oscillation energy decreases to one half
of its initial value in about 1 second. The frequency of middle C is 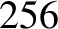 Hz. What
is the effective
Hz. What
is the effective  of the system? [Modified from French 1971.]
of the system? [Modified from French 1971.]
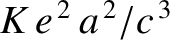 , where
, where
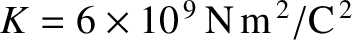 ,
, 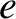 is the charge on an electron,
is the charge on an electron, 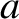 the instantaneous
acceleration, and
the instantaneous
acceleration, and 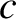 the velocity of light in vacuum (Fitzpatrick 2008).
the velocity of light in vacuum (Fitzpatrick 2008).
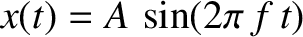 , how much energy
would it radiate away during a single cycle?
, how much energy
would it radiate away during a single cycle?
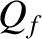 of this oscillator?
of this oscillator?
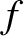 , give numerical estimates
for the
, give numerical estimates
for the 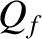 and half-life of the radiating system.
and half-life of the radiating system.
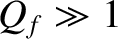 decays by a factor
decays by a factor
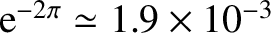 during
during 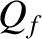 oscillation cycles. By what factor does the amplitude decay in the same time interval?
oscillation cycles. By what factor does the amplitude decay in the same time interval?
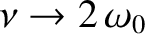 the solution to the damped
harmonic oscillator equation becomes
the solution to the damped
harmonic oscillator equation becomes
![$\displaystyle x(t) = \left(x_0 + \left[v_0+ \omega_0\,x_0\right]t\right){\rm e}^{-\omega_0\,t},
$](img641.png)
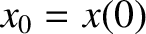 and
and
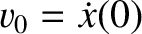 .
.
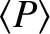 required to maintain a constant amplitude oscillation in a driven
damped harmonic oscillator can be calculated by recognizing that this power is minus the average rate that work is done by the damping force,
required to maintain a constant amplitude oscillation in a driven
damped harmonic oscillator can be calculated by recognizing that this power is minus the average rate that work is done by the damping force,
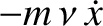 .
.
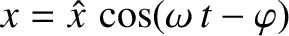 , show that the average rate that the damping force does work is
, show that the average rate that the damping force does work is
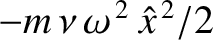 .
.
 at an arbitrary driving frequency and, hence, obtain an expression for
at an arbitrary driving frequency and, hence, obtain an expression for
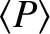 .
.
 governs the motion of an undamped harmonic oscillator driven by a sinusoidal
force of angular frequency
governs the motion of an undamped harmonic oscillator driven by a sinusoidal
force of angular frequency  .
.

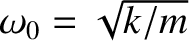 . Sketch the behavior of
. Sketch the behavior of  versus
versus  for
for
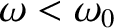 and
and
 .
.
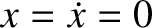 at
at  then the
general solution is
then the
general solution is
![$\displaystyle x =\frac{ F_0}{m\,(\omega_0^{\,2}-\omega^{\,2})}\left[\sin(\omega\,t)-\frac{\omega}{\omega_0}\,\sin(\omega_0\,t)\right].
$](img653.png)
 is close to the resonant frequency
is close to the resonant frequency  then
then
![$\displaystyle x\simeq \frac{F_0}{2\,m\,\omega_0^{\,2}}\left[\sin(\omega_0\,t)-\omega_0\,t\,\cos(\omega_0\,t)\right].
$](img654.png)
 versus
versus  .
.