Next: Multi-Slit Diffraction Up: Wave Optics Previous: One-Dimensional Fourier Optics Contents
 ,
and extend from
,
and extend from
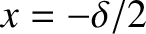 to
to
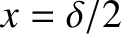 . The associated aperture function is
It follows from Equation (10.52) that
where
. The associated aperture function is
It follows from Equation (10.52) that
where
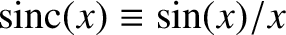 . Finally, assuming, for the sake of simplicity, that
. Finally, assuming, for the sake of simplicity, that
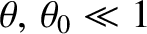 ,
which is most likely to be the case when
,
which is most likely to be the case when
 , the diffraction
pattern appearing on the projection screen is specified by
According to L'Hopital's rule,
, the diffraction
pattern appearing on the projection screen is specified by
According to L'Hopital's rule,
 .
Furthermore, it is easily demonstrated that the zeros of the
.
Furthermore, it is easily demonstrated that the zeros of the
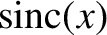 function occur at
function occur at 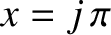 , where
, where 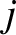 is a non-zero integer.
is a non-zero integer.
Figure 10.10 shows a typical single-slit diffraction pattern calculated for a case in which the slit width
greatly exceeds the wavelength of the light. The pattern consists of a dominant central maximum, flanked by subsidiary maxima of
fairly negligible amplitude.
The situation is shown schematically in Figure 10.11. When the incident
plane wave, whose direction of propagation subtends an angle 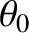 with the
with the 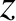 -axis, passes through the
slit it is effectively transformed into a divergent beam of light (the beam corresponds to the central peak in Figure 10.10) that is centered on
-axis, passes through the
slit it is effectively transformed into a divergent beam of light (the beam corresponds to the central peak in Figure 10.10) that is centered on
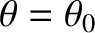 . The angle of
divergence of the beam, which is obtained from the first zero of the single-slit diffraction function (10.56), is
. The angle of
divergence of the beam, which is obtained from the first zero of the single-slit diffraction function (10.56), is
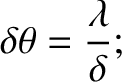 |
(10.57) |
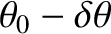 to
to
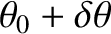 .
Thus, if the slit width,
.
Thus, if the slit width,  , is very much greater than the wavelength,
, is very much greater than the wavelength, 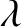 , of the light then the beam divergence is negligible, and the beam is, thus, governed by the laws of geometric optics (according to which there is no beam divergence).
On the other hand, if the slit width is comparable with the wavelength of the light then the beam divergence is significant, and the behavior of the beam is, consequently, very different to that predicted by the laws of
geometric optics.
, of the light then the beam divergence is negligible, and the beam is, thus, governed by the laws of geometric optics (according to which there is no beam divergence).
On the other hand, if the slit width is comparable with the wavelength of the light then the beam divergence is significant, and the behavior of the beam is, consequently, very different to that predicted by the laws of
geometric optics.
The diffraction of light is an important physical phenomenon because it sets a limit on the angular resolution of optical instruments. For instance, consider a
telescope whose objective lens is of diameter 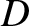 . When a plane wave from a distant light source of negligible angular
extent (e.g., a star) enters the lens it is diffracted, and forms a divergent beam of angular width
. When a plane wave from a distant light source of negligible angular
extent (e.g., a star) enters the lens it is diffracted, and forms a divergent beam of angular width 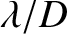 .
Thus, instead of being a point, the resulting image of the star is a disk of finite angular width
.
Thus, instead of being a point, the resulting image of the star is a disk of finite angular width 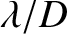 . (See Section 10.9.)
Suppose that two stars are an angular distance
. (See Section 10.9.)
Suppose that two stars are an angular distance
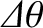 apart in the sky. As we have just seen, when viewed through
the telescope, each star appears as a disk of angular extent
apart in the sky. As we have just seen, when viewed through
the telescope, each star appears as a disk of angular extent
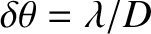 . If
. If
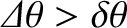 then
the two stars appear as separate disks. On the other hand, if
then
the two stars appear as separate disks. On the other hand, if
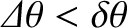 then the two
disks merge to form a single disk, and it becomes impossible to tell that there are, in fact, two stars.
It follows that the
minimum angular resolution of a telescope whose objective lens is of diameter
then the two
disks merge to form a single disk, and it becomes impossible to tell that there are, in fact, two stars.
It follows that the
minimum angular resolution of a telescope whose objective lens is of diameter 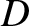 is
is
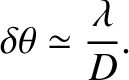 |
(10.58) |
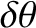 decreases) as the diameter of its objective lens increases.
decreases) as the diameter of its objective lens increases.