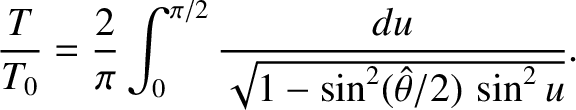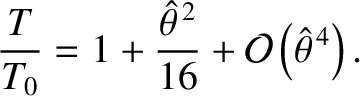Next: Damped and Driven Harmonic Up: Simple Harmonic Oscillation Previous: Compound Pendulum Contents
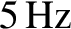 . Show that the mass loses contact with the platform
when the displacement exceeds
. Show that the mass loses contact with the platform
when the displacement exceeds
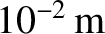 . [From Pain 1999.]
. [From Pain 1999.]
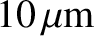 , at all frequencies, find the greatest
frequency (in hertz) for which the small body stays in contact with the diaphragm.
, at all frequencies, find the greatest
frequency (in hertz) for which the small body stays in contact with the diaphragm.
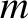 is attached to the mid-point of a stretched string of negligible mass, length
is attached to the mid-point of a stretched string of negligible mass, length 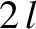 ,
and uniform tension
,
and uniform tension 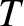 . Let
. Let 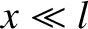 be the transverse displacement of the mass from its
equilibrium position. Show that the displacement executes simple harmonic oscillation at the
angular frequency
be the transverse displacement of the mass from its
equilibrium position. Show that the displacement executes simple harmonic oscillation at the
angular frequency
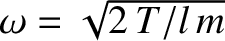 .
.
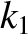 and
and 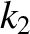 , respectively, and are used in a vertical
orientation to support an object of mass
, respectively, and are used in a vertical
orientation to support an object of mass 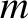 . Show that the angular frequency of small amplitude oscillations about the equilibrium state
is
. Show that the angular frequency of small amplitude oscillations about the equilibrium state
is
![$[(k_1+k_2)/m]^{1/2}$](img365.png) if the springs are connected in parallel, and
if the springs are connected in parallel, and
![$[k_1\,k_2/(k_1+k_2)\,m]^{1/2}$](img366.png) if the springs are connected in series.
if the springs are connected in series.
 is suspended at the end of a uniform spring of unstretched length
is suspended at the end of a uniform spring of unstretched length 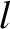 and spring constant
and spring constant  . If the
mass of the spring is
. If the
mass of the spring is 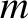 and the velocity of an element
and the velocity of an element 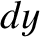 of its length is proportional to its
distance
of its length is proportional to its
distance  from the fixed end of the spring, show that the kinetic energy of this element
is
from the fixed end of the spring, show that the kinetic energy of this element
is
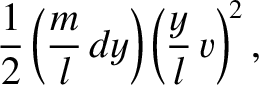
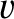 is the velocity of the suspended mass. Hence, by integrating over the length of the spring, show
that its total kinetic energy is
is the velocity of the suspended mass. Hence, by integrating over the length of the spring, show
that its total kinetic energy is
 . Finally, deduce, from energy conservation arguments, that the
angular oscillation frequency of the system is given by
. Finally, deduce, from energy conservation arguments, that the
angular oscillation frequency of the system is given by

 and mass density
and mass density 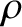 floats in a liquid
of density
floats in a liquid
of density  (where
(where
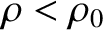 ), and at equilibrium displaces a volume
), and at equilibrium displaces a volume 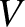 . Making use of Archimedes' principle (that the buoyancy force acting on a partially
submerged body is equal to the weight of the displaced liquid), show
that the period of small amplitude oscillations about the equilibrium position is
. Making use of Archimedes' principle (that the buoyancy force acting on a partially
submerged body is equal to the weight of the displaced liquid), show
that the period of small amplitude oscillations about the equilibrium position is
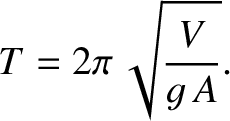
 consists of a horizontal section connected at either end to two vertical sections.
Suppose that the tube is filled with an incompressible liquid of mass density
consists of a horizontal section connected at either end to two vertical sections.
Suppose that the tube is filled with an incompressible liquid of mass density 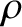 . Let the total length of the liquid column be
. Let the total length of the liquid column be 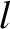 . (Where
. (Where 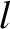 exceeds the length of the horizontal section.) Suppose that the surface of the liquid in one of the vertical sections is initially displaced (vertically) a
small distance
exceeds the length of the horizontal section.) Suppose that the surface of the liquid in one of the vertical sections is initially displaced (vertically) a
small distance 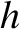 from its equilibrium position. Show that the surface displacement subsequently executes simple harmonic oscillation at the
angular frequency
from its equilibrium position. Show that the surface displacement subsequently executes simple harmonic oscillation at the
angular frequency
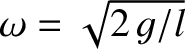 , where
, where 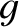 is the acceleration due to gravity.
is the acceleration due to gravity.
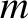 slides in a frictionless semi-circular depression in the
ground
of radius
slides in a frictionless semi-circular depression in the
ground
of radius 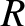 . Find the angular frequency of small amplitude oscillations
about the particle's equilibrium position, assuming that the oscillations
are essentially one-dimensional, so that the particle passes through
the lowest point of the depression during each oscillation cycle.
. Find the angular frequency of small amplitude oscillations
about the particle's equilibrium position, assuming that the oscillations
are essentially one-dimensional, so that the particle passes through
the lowest point of the depression during each oscillation cycle.
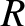 and uniform mass density. A particle is dropped into the tunnel from the surface.
Show that the particle undergoes simple harmonic oscillation at the angular
frequency
and uniform mass density. A particle is dropped into the tunnel from the surface.
Show that the particle undergoes simple harmonic oscillation at the angular
frequency
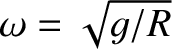 , where
, where 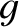 is the gravitational acceleration at Earth's surface.
(Hint: The gravitational acceleration at a point inside a spherically symmetric mass distribution
is the same as if all of the mass interior to the point were concentrated at the center, and
all of the mass exterior to the point were neglected.) Estimate how long it takes the particle to
reach the other end of the tunnel.
is the gravitational acceleration at Earth's surface.
(Hint: The gravitational acceleration at a point inside a spherically symmetric mass distribution
is the same as if all of the mass interior to the point were concentrated at the center, and
all of the mass exterior to the point were neglected.) Estimate how long it takes the particle to
reach the other end of the tunnel.
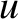 and
and 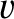 at displacements
at displacements
 and
and 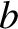 , respectively, from its equilibrium position.
, respectively, from its equilibrium position.

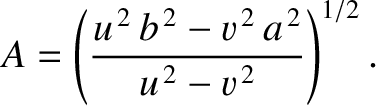
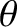 then a restoring
torque
then a restoring
torque
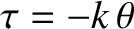 develops, where
develops, where 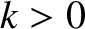 is known as the torsional
force constant. Consider a so-called torsional pendulum,
which consists of a horizontal disk of mass
is known as the torsional
force constant. Consider a so-called torsional pendulum,
which consists of a horizontal disk of mass  , and moment of inertia
, and moment of inertia 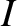 , suspended at its
center from a thin vertical wire of negligible mass and length
, suspended at its
center from a thin vertical wire of negligible mass and length 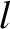 , whose other end is attached to a fixed
support. The disk is free to rotate about a vertical axis passing through the suspension point, but such rotation twists the wire. Find the frequency of torsional oscillations of the disk about its
equilibrium position.
, whose other end is attached to a fixed
support. The disk is free to rotate about a vertical axis passing through the suspension point, but such rotation twists the wire. Find the frequency of torsional oscillations of the disk about its
equilibrium position.
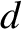 hangs on a nail. What is the period of its small amplitude oscillations? [From French 1971.]
hangs on a nail. What is the period of its small amplitude oscillations? [From French 1971.]
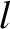 that pivots about one of its
ends. Show that the pendulum has the same period of oscillation as a simple pendulum of
length
that pivots about one of its
ends. Show that the pendulum has the same period of oscillation as a simple pendulum of
length 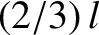 .
.
 that is
free to turn about a horizontal axis perpendicular to its plane. Find the position
of the axis for which the periodic time is a minimum.
that is
free to turn about a horizontal axis perpendicular to its plane. Find the position
of the axis for which the periodic time is a minimum.
 has a moment of inertia
has a moment of inertia  about a perpendicular axis passing
through its center of mass. Suppose that the object is converted into a compound pendulum by
suspending it about a horizontal axis perpendicular to its plane. Show that the minimum effective
length of the pendulum occurs when the distance of the suspension point from the
center of gravity is equal to the radius of gyration,
about a perpendicular axis passing
through its center of mass. Suppose that the object is converted into a compound pendulum by
suspending it about a horizontal axis perpendicular to its plane. Show that the minimum effective
length of the pendulum occurs when the distance of the suspension point from the
center of gravity is equal to the radius of gyration,
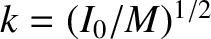 .
.
 and radius
and radius  rolls without slipping over a rough horizontal surface. Suppose that a small
mass
rolls without slipping over a rough horizontal surface. Suppose that a small
mass  is attached to the edge of the disk. Show that the angular frequency of small amplitude oscillations of the disk
about its equilibrium position is
is attached to the edge of the disk. Show that the angular frequency of small amplitude oscillations of the disk
about its equilibrium position is
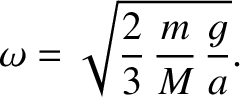
 times the maximum speed. [From Ingard 1988.]
times the maximum speed. [From Ingard 1988.]
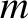 executes one-dimensional simple harmonic oscillation such that its instantaneous
executes one-dimensional simple harmonic oscillation such that its instantaneous  coordinate is
coordinate is

 ,
,  ,
, 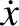 , and
, and
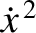 over a single cycle of the
oscillation.
over a single cycle of the
oscillation.
 -
- plane are
plane are
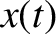 |
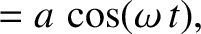 |
|
 |
 |
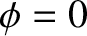 , (b)
, (b)
 , and (c)
, and (c)
 .
In each case, plot the trajectory of the particle in the
.
In each case, plot the trajectory of the particle in the  -
- plane.
plane.
 the capacitor is uncharged and a
current
the capacitor is uncharged and a
current  flows through the inductor. Find an expression for the
charge
flows through the inductor. Find an expression for the
charge 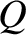 stored on the positive plate of the capacitor as a function of time.
stored on the positive plate of the capacitor as a function of time.
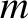 and length
and length 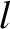 is such that
is such that
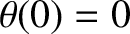 and
and
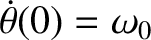 .
Find the subsequent motion,
.
Find the subsequent motion,  , assuming that
its amplitude remains small.
, assuming that
its amplitude remains small.
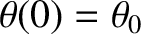 and
and
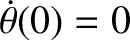 . Find the subsequent motion.
. Find the subsequent motion.
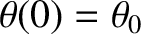 and
and
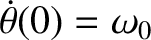 . Find the subsequent motion.
. Find the subsequent motion.
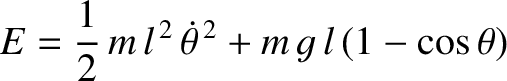
 , can be written
, can be written


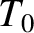 is the period of small-angle oscillations.
is the period of small-angle oscillations.
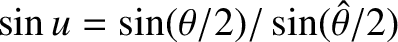 , show that the
previous expression transforms to
, show that the
previous expression transforms to