Next: Parallel EM Waves in Up: Dispersive Waves Previous: Electromagnetic Waves in Magnetized Contents
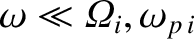 ),
we have [see Equations (9.124), (9.131), (9.138), (9.170), and (9.171)]
),
we have [see Equations (9.124), (9.131), (9.138), (9.170), and (9.171)]
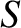 |
 |
(9.172) |
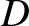 |
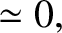 |
(9.173) |
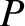 |
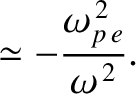 |
(9.174) |
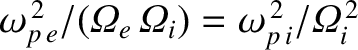 .
Thus, the eigenmode equation (9.168) reduces to
.
Thus, the eigenmode equation (9.168) reduces to
The solubility condition (Riley 1974) for the homogeneous matrix equation (9.175) yields the dispersion relation
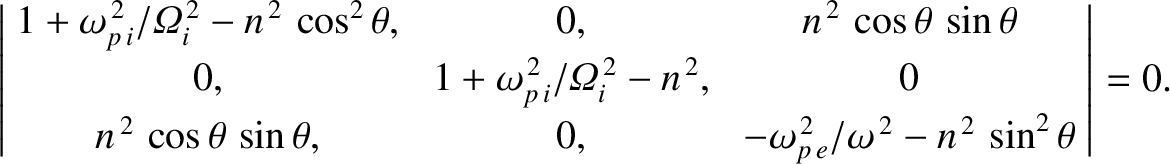 |
(9.176) |
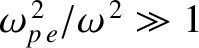 ,
,
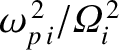 . Thus, we can see that the bottom
right-hand element of the previous determinant is far larger than any of the other
elements. Hence, to a good approximation, the roots of the dispersion relation
are obtained
by equating the term multiplying this large factor to zero. In this manner,
we obtain two roots:
and
. Thus, we can see that the bottom
right-hand element of the previous determinant is far larger than any of the other
elements. Hence, to a good approximation, the roots of the dispersion relation
are obtained
by equating the term multiplying this large factor to zero. In this manner,
we obtain two roots:
and
It is fairly easy to show, from the definitions of the plasma and cyclotron frequencies [see Equations (9.117)–(9.120)], that
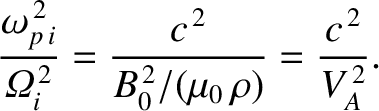 |
(9.179) |
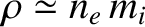 is the plasma mass density, and
is the plasma mass density, and
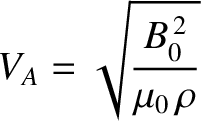 |
(9.180) |
 in a conventional plasma.
in a conventional plasma.
The dispersion relation (9.181) corresponds to the so-called shear-Alfvén wave, whereas the dispersion relation (9.182) corresponds to the compressional-Alfvén wave. The shear-Alfvén wave bends magnetic field-lines without compressing them, whereas the compressional-Alfvén wave compresses magnetic field-lines without bending them. Likewise, the shear-Alfvén wave does not compress the plasma, whereas the compressional-Alfvén wave does (Hazeltine and Waelbroeck 2004).
The shear-Alfvén wave is analogous to a wave on a string in tension, which propagates at the
phase velocity
 , where
, where 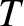 is the tension, and
is the tension, and 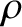 the linear mass density. (See Section 6.3.) At low frequencies, the plasma and the magnetic field are “tied” (i.e., if one moves then so
must the other), so it is possible to consider a magnetic field-line to be “loaded” with a plasma of
density
the linear mass density. (See Section 6.3.) At low frequencies, the plasma and the magnetic field are “tied” (i.e., if one moves then so
must the other), so it is possible to consider a magnetic field-line to be “loaded” with a plasma of
density 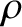 (Fitzpatrick 2015). Furthermore, in terms of the Maxwell stress tensor, the field-line is under a
tension
(Fitzpatrick 2015). Furthermore, in terms of the Maxwell stress tensor, the field-line is under a
tension
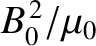 (Fitzpatrick 2008). Hence,
(Fitzpatrick 2008). Hence,
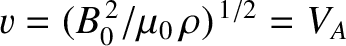 . We, thus, obtain the correct
result for waves propagating along the magnetic field. The compressional-Alfvén wave is
similar to a conventional sound wave (see Section 5.4), except that the restoring force
emanates from magnetic pressure, rather than the thermal pressure of the plasma (which has actually
been neglected in the present analysis) (Fitzpatrick 2015).
. We, thus, obtain the correct
result for waves propagating along the magnetic field. The compressional-Alfvén wave is
similar to a conventional sound wave (see Section 5.4), except that the restoring force
emanates from magnetic pressure, rather than the thermal pressure of the plasma (which has actually
been neglected in the present analysis) (Fitzpatrick 2015).