Next: Traveling Waves Up: Longitudinal Standing Waves Previous: Fourier Analysis Contents
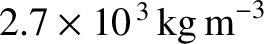 ,
,
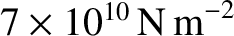 , and
, and
 , respectively. (Assume, for the sake of simplicity, that aluminum has a simple cubic lattice.)
, respectively. (Assume, for the sake of simplicity, that aluminum has a simple cubic lattice.)
 and
and  , where
, where 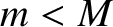 . The masses are connected by identical chemical bonds that are
modeled as springs of spring constant
. The masses are connected by identical chemical bonds that are
modeled as springs of spring constant 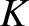 .
.
 or in the band
or in the band
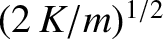 to
to
![$[2\,K\,(1/M+1/m)]^{1/2}$](img1305.png) .
.
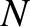 identical simple pendula of mass
identical simple pendula of mass 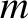 and
length
and
length 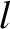 that are suspended from equal-height points, evenly-spaced a distance
that are suspended from equal-height points, evenly-spaced a distance  apart. Suppose that each pendulum bob is attached to
its two immediate neighbors by means of light springs of unstretched
length
apart. Suppose that each pendulum bob is attached to
its two immediate neighbors by means of light springs of unstretched
length  and spring constant
and spring constant 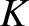 . Figure 5.8 shows a small part of
such an array. Let
. Figure 5.8 shows a small part of
such an array. Let 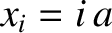 be the equilibrium position of the
be the equilibrium position of the 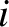 th bob, for
th bob, for
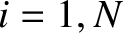 , and let
, and let  be its horizontal displacement. It is assumed that
be its horizontal displacement. It is assumed that
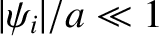 for
all
for
all 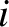 .
.
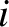 th pendulum bob is
th pendulum bob is
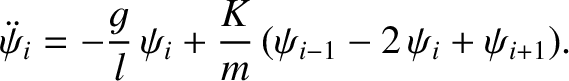
![$\displaystyle \psi_i(t) = [A\,\sin (k\,x_i)+ B\,\cos(k\,x_i)]\,\cos(\omega\,t-\phi).
$](img1308.png)
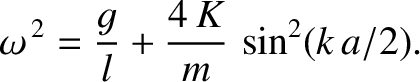
 away, by means of light springs of unstretched length
away, by means of light springs of unstretched length  and spring constant
and spring constant 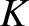 . Find the normal modes of the system.
. Find the normal modes of the system.
 of period
of period  , where
, where
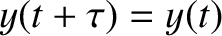 for
all
for
all  , which is represented as a Fourier series,
, which is represented as a Fourier series,
![$\displaystyle y(t) = C_0 + \sum_{n>0}\left[C_n\,\cos(n\,\omega\,t) + S_n\,\sin(n\,\omega\,t)\right],
$](img1311.png)
 .
.
![$\displaystyle y(-t) = C_0 + \sum_{n>0}\left[C_n'\,\cos(n\,\omega\,t) + S_n'\,\sin(n\,\omega\,t)\right],
$](img1312.png)
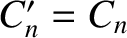 and
and 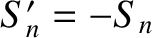 .
.
![$\displaystyle y(t+T) = C_0 + \sum_{n>0}\left[C_n''\,\cos(n\,\omega\,t) + S_n''\,\sin(n\,\omega\,t)\right],
$](img1315.png)
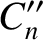 |
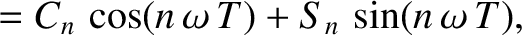 |
|
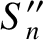 |
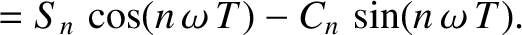 |
![$\displaystyle y(t)=A\left\{\begin{array}{ccc}
-1&\mbox{\hspace{1cm}}&0\leq t/\tau\leq 1/2\\ [0.5ex]
+1 &&1/2<t/\tau \leq 1
\end{array}\right.,
$](img1320.png)
 for all
for all  , has the Fourier representation
, has the Fourier representation
![$\displaystyle y(t) = -\frac{4\,A}{\pi}\left[\frac{\sin(\omega\,t)}{1}+ \frac{\sin(3\,\omega\,t)}{3}+ \frac{\sin(5\,\omega\,t)}{5}+\cdots\right].
$](img1321.png)
 . Plot the reconstructed waveform, retaining the first 4, 8, 16, and
32 terms in the Fourier series.
. Plot the reconstructed waveform, retaining the first 4, 8, 16, and
32 terms in the Fourier series.
![$\displaystyle y(t)=A\left\{\begin{array}{ccl}
1&\mbox{\hspace{1cm}}&\vert t-T/2\vert\leq \tau/2\\ [0.5ex]
0 &&\mbox{otherwise}
\end{array}\right.,
$](img1322.png)
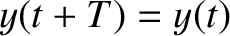 for all
for all  , and
, and 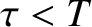 , has the Fourier representation
, has the Fourier representation
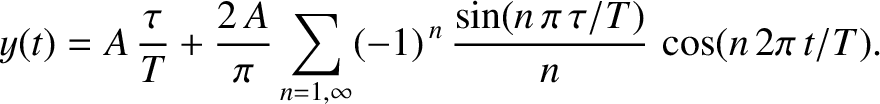
 then the most significant terms in the preceding series have
frequencies (in hertz) that range from the fundamental frequency
then the most significant terms in the preceding series have
frequencies (in hertz) that range from the fundamental frequency 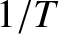 to a frequency
of order
to a frequency
of order  .
.