


Next: Lenz's Law
Up: Magnetic Induction
Previous: Magnetic Induction
The phenomenon of magnetic induction plays a crucial role in
three very useful electrical devices: the electric generator, the electric
motor, and the transformer. Without these devices, modern life would be
impossible in its present form. Magnetic induction was discovered in 1830 by the
English physicist Michael Faraday. The American physicist Joseph Henry
independently made the same discovery at about the same time. Both
physicists were intrigued by the fact that an electric current flowing around
a circuit can generate a magnetic field. Surely, they reasoned, if an electric
current can generate a magnetic field then a magnetic field must somehow be able to
generate an electric current.
However, it took many years of fruitless experimentation
before they were able to find the essential ingredient which allows
a magnetic field to generate an electric current. This
ingredient is time variation.
Consider a planar loop 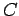 of conducting wire of cross-sectional area
of conducting wire of cross-sectional area  .
Let us place this loop in a magnetic field whose strength
.
Let us place this loop in a magnetic field whose strength 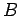 is approximately
uniform over the extent of the loop. Suppose that the direction of the
magnetic field subtends an angle
is approximately
uniform over the extent of the loop. Suppose that the direction of the
magnetic field subtends an angle 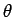 with the normal direction to the
loop. The magnetic flux
with the normal direction to the
loop. The magnetic flux 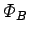 through the loop is
defined as the product of the area of the loop and the component of
the magnetic field perpendicular to the loop. Thus,
through the loop is
defined as the product of the area of the loop and the component of
the magnetic field perpendicular to the loop. Thus,
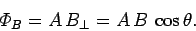 |
(191) |
If the loop is wrapped around itself  times (i.e., if the loop
has
times (i.e., if the loop
has  turns) then the magnetic flux through the loop is simply
turns) then the magnetic flux through the loop is simply
 times the magnetic flux through a single turn:
times the magnetic flux through a single turn:
 |
(192) |
Finally, if the magnetic field is not uniform over the loop, or the loop does not
lie in one plane,
then we must evaluate the
magnetic flux as a surface integral
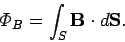 |
(193) |
Here, 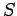 is some surface attached to
is some surface attached to 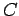 .
If the loop has
.
If the loop has  turns then the flux is
turns then the flux is  times the above value.
The SI unit of magnetic flux is the weber (Wb). One tesla is equivalent to
one weber per meter squared:
times the above value.
The SI unit of magnetic flux is the weber (Wb). One tesla is equivalent to
one weber per meter squared:
 |
(194) |
Faraday discovered that if the magnetic field through a loop of wire
varies in time then an emf is induced around the loop.
Faraday was able to observe this effect because the emf gives rise to
a current circulating in the loop. Faraday found that the magnitude of
the emf is directly proportional to the time rate of change of the magnetic field.
He also discovered that an emf is generated when a loop of wire moves
from a region of low magnetic field-strength to one of high magnetic field-strength, and vice versa. The emf is directly proportional to
the velocity with which the loop moves between the two regions. Finally,
Faraday discovered that an emf is generated around a loop which rotates
in a uniform magnetic field of constant strength. In this case, the emf
is directly proportional to the rate at which the loop rotates.
Faraday was eventually
able to propose a single
law which could account for all of his many and varied observations. This law, which is known as
Faraday's law of magnetic induction, is as follows:
The emf induced in a circuit is proportional to the time rate of change of the
magnetic flux linking that circuit.
SI units have been fixed so that the constant of proportionality in this
law is unity. Thus, if the magnetic flux through a circuit changes
by an amount 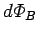 in a time interval
in a time interval 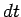 then the emf
then the emf 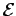 generated in the circuit is
generated in the circuit is
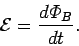 |
(195) |
There are many different ways in which the magnetic flux linking an
electric circuit can
change. Either the magnetic field-strength can change, or the direction of the magnetic
field can change, or the position of the circuit can change, or the shape of the
circuit can change, or the orientation of the circuit can change.
Faraday's law states that all of these ways are
completely equivalent as far as the generation of an emf around the
circuit is concerned.



Next: Lenz's Law
Up: Magnetic Induction
Previous: Magnetic Induction
Richard Fitzpatrick
2007-07-14
![]() of conducting wire of cross-sectional area
of conducting wire of cross-sectional area ![]() .
Let us place this loop in a magnetic field whose strength
.
Let us place this loop in a magnetic field whose strength ![]() is approximately
uniform over the extent of the loop. Suppose that the direction of the
magnetic field subtends an angle
is approximately
uniform over the extent of the loop. Suppose that the direction of the
magnetic field subtends an angle ![]() with the normal direction to the
loop. The magnetic flux
with the normal direction to the
loop. The magnetic flux ![]() through the loop is
defined as the product of the area of the loop and the component of
the magnetic field perpendicular to the loop. Thus,
through the loop is
defined as the product of the area of the loop and the component of
the magnetic field perpendicular to the loop. Thus,