


Next: Magnetic Field of a
Up: Magnetism
Previous: The Hall Effect
Ampère's Circuital Law
Consider a long thin wire carrying a steady current 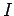 . Suppose that the
wire is orientated such that the current flows along the
. Suppose that the
wire is orientated such that the current flows along the 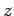 -axis.
Consider some closed loop
-axis.
Consider some closed loop 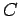 in the
in the  -
-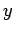 plane which circles the wire in
an anti-clockwise direction, looking down the
plane which circles the wire in
an anti-clockwise direction, looking down the 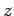 -axis. Suppose that
-axis. Suppose that
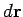 is a short straight-line element of this loop.
Let us form the dot product of this element with the local magnetic field
is a short straight-line element of this loop.
Let us form the dot product of this element with the local magnetic field
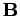 . Thus,
. Thus,
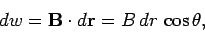 |
(173) |
where 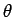 is the angle subtended between the direction of the line element and
the direction of the local magnetic field. We can calculate a
is the angle subtended between the direction of the line element and
the direction of the local magnetic field. We can calculate a 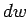 for
every line element which makes up the loop
for
every line element which makes up the loop 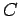 . If we sum all of the
. If we sum all of the
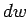 values thus obtained, and take the limit as the
number of elements goes to infinity,
we obtain the line integral
values thus obtained, and take the limit as the
number of elements goes to infinity,
we obtain the line integral
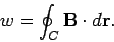 |
(174) |
What is the value of this
integral? In general, this is a difficult question
to answer. However, let us consider a special case. Suppose that 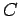 is a circle
of radius
is a circle
of radius 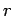 centred on the wire. In this case, the magnetic field-strength
is the same at all points on the loop. In fact,
centred on the wire. In this case, the magnetic field-strength
is the same at all points on the loop. In fact,
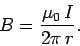 |
(175) |
Moreover, the field is everywhere parallel to the line elements which
make up the loop. Thus,
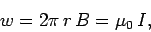 |
(176) |
or
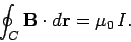 |
(177) |
In other words, the line integral of the magnetic field around some
circular loop  , centred on a current carrying wire, and
in the plane perpendicular to the wire, is equal to
, centred on a current carrying wire, and
in the plane perpendicular to the wire, is equal to 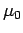 times the current flowing in the wire. Note that this answer is independent of
the radius
times the current flowing in the wire. Note that this answer is independent of
the radius 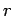 of the loop: i.e., the same result is
obtained by taking the line integral around any circular loop centred
on the wire.
of the loop: i.e., the same result is
obtained by taking the line integral around any circular loop centred
on the wire.
In 1826, Ampère demonstrated that Eq. (177) holds for any closed loop which
circles around any distribution of currents. Thus, Ampère's circuital law
can be written:
The line integral of the magnetic field around some closed loop
is equal to the 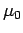 times the algebraic sum of the currents which pass through the
loop.
times the algebraic sum of the currents which pass through the
loop.
In forming the algebraic sum of the currents passing through the loop, those currents
which the loop circles in an anti-clockwise direction (looking
against the direction of the current) count as positive currents, whereas those
which the loop circles in a clockwise direction (looking
against the direction of the current) count as negative currents.
Ampère's circuital law is to magnetostatics (the study of the magnetic fields
generated by steady currents) what Gauss' law is to electrostatics
(the study of the electric fields generated by stationary charges). Like
Gauss' law, Ampère's circuital law is particularly useful in situations
which possess a high degree of symmetry.



Next: Magnetic Field of a
Up: Magnetism
Previous: The Hall Effect
Richard Fitzpatrick
2007-07-14
![]() is a circle
of radius
is a circle
of radius ![]() centred on the wire. In this case, the magnetic field-strength
is the same at all points on the loop. In fact,
centred on the wire. In this case, the magnetic field-strength
is the same at all points on the loop. In fact,
times the algebraic sum of the currents which pass through the loop.