Ampère's Experiments

In 1820, the Danish physicist Hans Christian Ørsted was giving a lecture demonstration of various electrical and magnetic effects. Suddenly, much to his amazement, he noticed that the needle of a compass he was holding was deflected when he moved it close to a current carrying wire. This was a very surprising observation, since, until that moment, electricity and magnetism had been thought of as two quite unrelated phenomena. Word of this discovery spread quickly along the scientific grapevine, and the French physicist Andre Marie Ampère immediately decided to investigate further. Ampère's apparatus consisted (essentially) of a long straight wire carrying an electric current current $I$. Ampère quickly discovered that the needle of a small compass maps out a series of concentric circular loops in the plane perpendicular to a current carrying wire--see Fig. 20. The direction of circulation around these magnetic loops is conventionally taken to be the direction in which the north pole of a compass needle points. Using this convention, the circulation of the loops is given by a right-hand rule. If the thumb of the right-hand points along the direction of the current, then the fingers of the right-hand circulate in the same sense as the magnetic loops.

Figure 20: Magnetic loops around a current carrying wire.

Ampère's next series of experiments involved bringing a short test wire, carrying a current $I'$, close to the original wire, and investigating the force exerted on the test wire. This experiment is not quite as clear cut as Coulomb's experiment because, unlike electric charges, electric currents cannot exist as point entities. They have to flow in complete circuits. We must imagine that the circuit which connects with the central wire is sufficiently far away that it has no appreciable influence on the outcome of the experiment. The circuit which connects with the test wire is more problematic. Fortunately, if the feed wires are twisted around each other, as indicated in Fig. 21, then they effectively cancel one another out, and also do not influence the outcome of the experiment.

Figure 21: Ampère's experiment.

Ampère discovered that the force exerted on the test wire is directly proportional to its length. He also made the following observations. If the current in the test wire (i.e., the test current) flows parallel to the current in the central wire then the two wires attract one another. If the current in the test wire is reversed then the two wires repel one another. If the test current points radially towards the central wire (and the current in the central wire flows upward) then the test wire is subject to a downward force. If the test current is reversed then the force is upward. If the test current is rotated in a single plane, so that it starts parallel to the central current and ends up pointing radially towards it, then the force on the test wire is of constant magnitude, and is always at right-angles to the test current. If the test current is parallel to a magnetic loop then there is no force exerted on the test wire. If the test current is rotated in a single plane, so that it starts parallel to the central current, and ends up pointing along a magnetic loop, then the magnitude of the force on the test wire attenuates like $\cos\theta$ (where $\theta$ is the angle the current is turned through, and $\theta=0$ corresponds to the case where the test current is parallel to the central current), and its direction is again always at right-angles to the test current. Finally, Ampère was able to establish that the attractive force between two parallel current carrying wires is proportional to the product of the two currents, and falls off like one over the perpendicular distance between the wires.

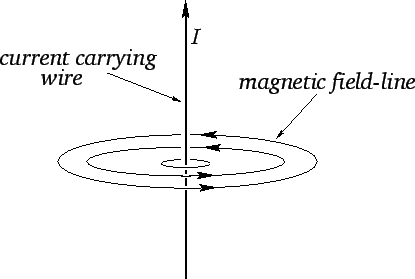
This rather complicated force law can be summed up succinctly in vector notation provided that we define a vector field ${\bf B}$, called the magnetic field, which fills space, and whose direction is everywhere tangential to the magnetic loops mapped out by the north pole of a small compass. The dependence of the force per unit length, ${\bf F}$, acting on a test wire with the different possible orientations of the test current is described by

$${\bf F} = {\bf I}' \times{\bf B},$$ (152)

where ${\bf I}'$ is a vector whose direction and magnitude are the same as those of the test current.

The variation of the force per unit length acting on a test wire with the strength of the central current, and the perpendicular distance $r$ to the central wire, is accounted for by saying that the magnetic field-strength is proportional to $I$, and inversely proportional to $r$. Thus, we can write

$$B = \frac{\mu_0\,I} {2 \pi\, r}.$$ (153)

The constant of proportionality $\mu_0$ is called the permeability of free space, and takes the value

$$\mu_0 = 4\pi \times 10^{-7}\,{\rm N\,A^{-2}}.$$ (154)

Incidentally, the SI unit of magnetic field strength is the tesla (T), which is the same as a newton per ampere per meter:

$$1\,{\rm T} \equiv 1\,{\rm N}\,{\rm A}^{-1}\,{\rm m}^{-1}.$$ (155)

The concept of a magnetic field which fills the space around a current carrying wire allows the calculation of the force on a test wire to be conveniently split into two parts. In the first part, we calculate the magnetic field generated by the current flowing in the central wire. This field circulates in the plane normal to the wire. Its magnitude is proportional to the central current, and inversely proportional to the perpendicular distance from the wire. In the second part, we use Eq. (152) to calculate the force per unit length acting on a short current carrying wire placed in the magnetic field generated by the central current. This force is perpendicular to both the direction of the magnetic field and the direction of the test current. Note that, at this stage, we have no reason to suppose that the magnetic field has any real existence. It is introduced merely to facilitate the calculation of the force exerted on the test wire by the central wire. It turns out, however, that the magnetic field does have a real existence, since, as we shall see, there is an energy associated with a magnetic field which fills space.