


Next: Resistors in Series and
Up: Electric Current
Previous: Resistance and Resistivity
Now, real batteries are constructed from materials which possess non-zero resistivities.
It follows that real batteries are not just pure voltage sources. They also possess
internal resistances.
Incidentally, a pure voltage
source is usually referred to as an emf (which stands for electromotive force). Of course,
emf is measured in units of volts.
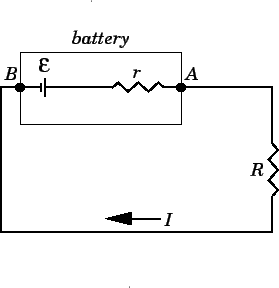
A battery can be modeled as an emf 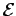 connected in series with a resistor
connected in series with a resistor
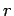 , which represents its internal resistance. Suppose that such
a battery is used to drive a current
, which represents its internal resistance. Suppose that such
a battery is used to drive a current 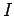 through an external load resistor
through an external load resistor 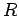 , as
shown in Fig. 17.
Note that in circuit diagrams an emf
, as
shown in Fig. 17.
Note that in circuit diagrams an emf 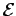 is represented as two closely spaced parallel
lines of unequal length. The electric potential of the longer line is greater than
that of the shorter one by
is represented as two closely spaced parallel
lines of unequal length. The electric potential of the longer line is greater than
that of the shorter one by  volts. A resistor is represented as
a zig-zag line.
volts. A resistor is represented as
a zig-zag line.
Figure 17:
A battery of emf 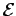 and internal resistance
and internal resistance 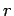 connected
to a load resistor of resistance
connected
to a load resistor of resistance 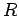 .
.
 |
Consider the battery in the figure. The voltage  of the battery is
defined as the difference in electric potential between its positive and
negative terminals: i.e., the points
of the battery is
defined as the difference in electric potential between its positive and
negative terminals: i.e., the points  and
and 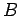 , respectively. As we move from
, respectively. As we move from 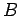 to
to
 , the electric potential increases by
, the electric potential increases by  volts as we cross the
emf, but then decreases by
volts as we cross the
emf, but then decreases by 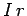 volts as we cross the internal resistor.
The voltage drop across the resistor follows from Ohm's law, which implies that
the drop in voltage across a resistor
volts as we cross the internal resistor.
The voltage drop across the resistor follows from Ohm's law, which implies that
the drop in voltage across a resistor 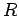 , carrying a current
, carrying a current
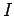 , is
, is 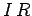 in the direction in which the
current flows. Thus, the voltage
in the direction in which the
current flows. Thus, the voltage  of the battery is related to its emf
of the battery is related to its emf
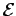 and internal resistance
and internal resistance 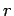 via
via
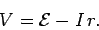 |
(133) |
Now, we usually think of the emf of a battery as being essentially constant (since it
only depends on the chemical reaction going on inside the battery, which converts
chemical energy into electrical energy), so we must conclude that the voltage of a
battery actually decreases as the current drawn from it increases.
In fact, the voltage only equals the
emf when the current is negligibly small. The current draw
from the battery cannot normally exceed the critical value
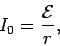 |
(134) |
since
for 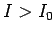 the voltage
the voltage  becomes negative (which can only happen
if the load resistor
becomes negative (which can only happen
if the load resistor 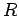 is also negative: this is essentially impossible).
It follows that if we short-circuit a battery, by connecting its
positive and negative terminals together using a conducting wire of negligible resistance,
the current drawn from the battery is limited by its internal resistance.
In fact, in this case, the current is equal to the maximum possible
current
is also negative: this is essentially impossible).
It follows that if we short-circuit a battery, by connecting its
positive and negative terminals together using a conducting wire of negligible resistance,
the current drawn from the battery is limited by its internal resistance.
In fact, in this case, the current is equal to the maximum possible
current
 .
.
A real battery is usually characterized in terms of
its emf 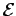 (i.e., its
voltage at zero current), and the maximum current
(i.e., its
voltage at zero current), and the maximum current  which it can supply.
For instance, a standard dry cell (i.e., the sort of
battery used to power calculators and torches) is usually rated at
which it can supply.
For instance, a standard dry cell (i.e., the sort of
battery used to power calculators and torches) is usually rated at 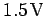 and (say)
and (say)  . Thus, nothing really catastrophic is going to
happen if we short-circuit a dry cell. We will run the battery down in a
comparatively short space of time, but no dangerously large current is going to
flow. On the other hand, a car battery is usually rated at
. Thus, nothing really catastrophic is going to
happen if we short-circuit a dry cell. We will run the battery down in a
comparatively short space of time, but no dangerously large current is going to
flow. On the other hand, a car battery is usually rated at  and something like
and something like 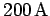 (this is the sort of current needed to
operate a starter motor). It is clear that a car battery must have a much
lower internal resistance than a dry cell. It follows that if
we were foolish enough to short-circuit a car battery the result would be
fairly catastrophic (imagine all of the energy needed to turn over the engine of
a car going into a thin wire connecting the battery terminals together).
(this is the sort of current needed to
operate a starter motor). It is clear that a car battery must have a much
lower internal resistance than a dry cell. It follows that if
we were foolish enough to short-circuit a car battery the result would be
fairly catastrophic (imagine all of the energy needed to turn over the engine of
a car going into a thin wire connecting the battery terminals together).



Next: Resistors in Series and
Up: Electric Current
Previous: Resistance and Resistivity
Richard Fitzpatrick
2007-07-14

![]() of the battery is
defined as the difference in electric potential between its positive and
negative terminals: i.e., the points
of the battery is
defined as the difference in electric potential between its positive and
negative terminals: i.e., the points ![]() and
and ![]() , respectively. As we move from
, respectively. As we move from ![]() to
to
![]() , the electric potential increases by
, the electric potential increases by ![]() volts as we cross the
emf, but then decreases by
volts as we cross the
emf, but then decreases by ![]() volts as we cross the internal resistor.
The voltage drop across the resistor follows from Ohm's law, which implies that
the drop in voltage across a resistor
volts as we cross the internal resistor.
The voltage drop across the resistor follows from Ohm's law, which implies that
the drop in voltage across a resistor ![]() , carrying a current
, carrying a current
![]() , is
, is ![]() in the direction in which the
current flows. Thus, the voltage
in the direction in which the
current flows. Thus, the voltage ![]() of the battery is related to its emf
of the battery is related to its emf
![]() and internal resistance
and internal resistance ![]() via
via
![]() (i.e., its
voltage at zero current), and the maximum current
(i.e., its
voltage at zero current), and the maximum current ![]() which it can supply.
For instance, a standard dry cell (i.e., the sort of
battery used to power calculators and torches) is usually rated at
which it can supply.
For instance, a standard dry cell (i.e., the sort of
battery used to power calculators and torches) is usually rated at ![]() and (say)
and (say) ![]() . Thus, nothing really catastrophic is going to
happen if we short-circuit a dry cell. We will run the battery down in a
comparatively short space of time, but no dangerously large current is going to
flow. On the other hand, a car battery is usually rated at
. Thus, nothing really catastrophic is going to
happen if we short-circuit a dry cell. We will run the battery down in a
comparatively short space of time, but no dangerously large current is going to
flow. On the other hand, a car battery is usually rated at ![]() and something like
and something like ![]() (this is the sort of current needed to
operate a starter motor). It is clear that a car battery must have a much
lower internal resistance than a dry cell. It follows that if
we were foolish enough to short-circuit a car battery the result would be
fairly catastrophic (imagine all of the energy needed to turn over the engine of
a car going into a thin wire connecting the battery terminals together).
(this is the sort of current needed to
operate a starter motor). It is clear that a car battery must have a much
lower internal resistance than a dry cell. It follows that if
we were foolish enough to short-circuit a car battery the result would be
fairly catastrophic (imagine all of the energy needed to turn over the engine of
a car going into a thin wire connecting the battery terminals together).