


Next: The Vector Product
Up: Vectors
Previous: Vector Area
A scalar quantity is invariant under all possible rotational transformations.
The individual components of a vector are not scalars because they change under
transformation. Can we form a scalar out of some combination of the components
of one, or more, vectors? Suppose that we were to define the
``ampersand'' product,
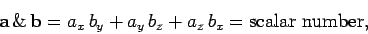 |
(16) |
for general vectors 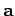 and
and 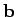 . Is
. Is
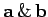 invariant under transformation, as must be the case if it is a scalar number?
Let us consider an example. Suppose that
invariant under transformation, as must be the case if it is a scalar number?
Let us consider an example. Suppose that
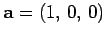 and
and
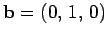 . It is easily seen that
. It is easily seen that
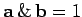 . Let
us now rotate the basis through
. Let
us now rotate the basis through 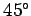 about the
about the 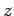 -axis. In the new
basis,
-axis. In the new
basis,
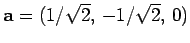 and
and
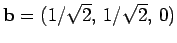 , giving
, giving
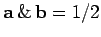 . Clearly,
. Clearly,
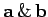 is not invariant under rotational transformation, so
the above definition is a bad one.
is not invariant under rotational transformation, so
the above definition is a bad one.
Consider, now,
the dot product or scalar product,
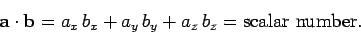 |
(17) |
Let us rotate the basis though 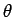 degrees about the
degrees about the 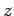 -axis. According to
Eqs. (10)-(12), in the new basis
-axis. According to
Eqs. (10)-(12), in the new basis
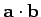 takes the form
takes the form
Thus,
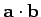 is invariant under rotation about the
is invariant under rotation about the 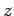 -axis. It can easily
be shown that it is also invariant under rotation about the
-axis. It can easily
be shown that it is also invariant under rotation about the  - and
- and 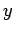 -axes.
Clearly,
-axes.
Clearly,
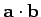 is a true scalar, so the above definition is
a good one. Incidentally,
is a true scalar, so the above definition is
a good one. Incidentally,
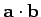 is the only
simple combination of
the components of two vectors which transforms like a scalar. It is easily
shown that the dot product is commutative and distributive:
is the only
simple combination of
the components of two vectors which transforms like a scalar. It is easily
shown that the dot product is commutative and distributive:
The associative property is meaningless for the dot product, because we cannot
have
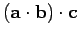 , since
, since
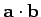 is scalar.
is scalar.
We have shown that the dot product
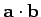 is coordinate independent.
But what is the physical significance of this? Consider the special case
where
is coordinate independent.
But what is the physical significance of this? Consider the special case
where
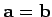 . Clearly,
. Clearly,
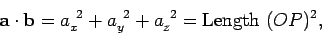 |
(20) |
if 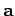 is the position vector of
is the position vector of 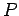 relative to the origin
relative to the origin 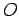 .
So, the invariance of
.
So, the invariance of
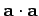 is equivalent to the invariance
of the length, or magnitude, of vector
is equivalent to the invariance
of the length, or magnitude, of vector 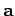 under transformation. The length of
vector
under transformation. The length of
vector 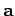 is usually denoted
is usually denoted 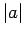 (``the modulus of
(``the modulus of 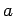 '') or sometimes
just
'') or sometimes
just 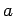 , so
, so
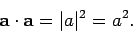 |
(21) |
Figure 5:
A vector triangle.
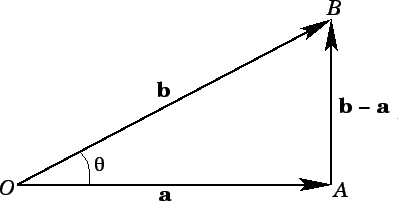 |
Let us now investigate the general case. The length squared of 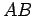 in Fig. 5 is
in Fig. 5 is
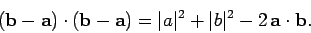 |
(22) |
However, according to the ``cosine rule'' of trigonometry,
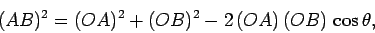 |
(23) |
where 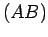 denotes the length of side
denotes the length of side 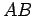 . It follows that
. It follows that
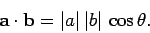 |
(24) |
Clearly, the invariance of
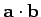 under transformation is equivalent
to the invariance of the angle subtended between the two vectors. Note that
if
under transformation is equivalent
to the invariance of the angle subtended between the two vectors. Note that
if
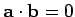 then either
then either 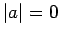 ,
, 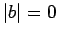 , or the vectors
, or the vectors
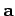 and
and 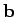 are mutually perpendicular. The angle
are mutually perpendicular. The angle 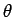 subtended between two vectors
can easily be obtained from the dot product: i.e.,
subtended between two vectors
can easily be obtained from the dot product: i.e.,
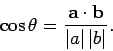 |
(25) |
Note that
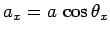 , etc., where
, etc., where 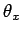 is
the angle subtended between vector
is
the angle subtended between vector 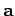 and the
and the  -axis.
-axis.
The work 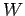 performed by a constant force
performed by a constant force 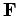 which moves an object through a displacement
which moves an object through a displacement 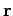 is the product of the magnitude of
is the product of the magnitude of 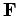 times the displacement in the direction
of
times the displacement in the direction
of 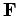 . So, if the angle subtended between
. So, if the angle subtended between 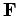 and
and 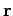 is
is 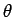 then
then
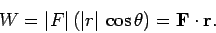 |
(26) |



Next: The Vector Product
Up: Vectors
Previous: Vector Area
Richard Fitzpatrick
2007-07-14
![]() is coordinate independent.
But what is the physical significance of this? Consider the special case
where
is coordinate independent.
But what is the physical significance of this? Consider the special case
where
![]() . Clearly,
. Clearly,
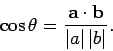
![]() performed by a constant force
performed by a constant force ![]() which moves an object through a displacement
which moves an object through a displacement ![]() is the product of the magnitude of
is the product of the magnitude of ![]() times the displacement in the direction
of
times the displacement in the direction
of ![]() . So, if the angle subtended between
. So, if the angle subtended between ![]() and
and ![]() is
is ![]() then
then