


Next: Worked Examples
Up: Capacitance
Previous: Capacitors in Series and
Let us consider charging an initially uncharged parallel plate
capacitor by transferring a charge 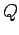 from one
plate to the other, leaving the former plate with charge
from one
plate to the other, leaving the former plate with charge 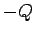 and the later
with charge
and the later
with charge 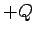 . Of course,
once we have transferred some charge, an electric field is set up between
the plates which opposes any further charge transfer. In order to fully
charge the capacitor, we must do
work against this field, and this work becomes
energy stored in the capacitor. Let us calculate this
energy.
. Of course,
once we have transferred some charge, an electric field is set up between
the plates which opposes any further charge transfer. In order to fully
charge the capacitor, we must do
work against this field, and this work becomes
energy stored in the capacitor. Let us calculate this
energy.
Suppose that the capacitor plates carry a charge 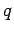 and that the
potential difference between the plates is
and that the
potential difference between the plates is  . The work we do in transferring
an infinitesimal amount of charge
. The work we do in transferring
an infinitesimal amount of charge  from the negative to the
positive plate is simply
from the negative to the
positive plate is simply
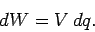 |
(117) |
In order to evaluate the total work 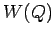 done in transferring
the total charge
done in transferring
the total charge 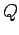 from one plate to the other, we can divide this charge into many small
increments
from one plate to the other, we can divide this charge into many small
increments  , find the incremental work
, find the incremental work
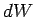 done in transferring this incremental charge,
using the above formula, and
then sum all of these works. The only complication is that the potential
difference
done in transferring this incremental charge,
using the above formula, and
then sum all of these works. The only complication is that the potential
difference  between the plates is a function of the total transferred
charge. In fact,
between the plates is a function of the total transferred
charge. In fact, 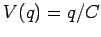 , so
, so
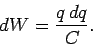 |
(118) |
Integration yields
 |
(119) |
Note, again, that the work 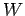 done in charging the capacitor is
the same as the energy stored in the capacitor. Since
done in charging the capacitor is
the same as the energy stored in the capacitor. Since 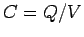 , we can
write this stored energy in one of three equivalent forms:
, we can
write this stored energy in one of three equivalent forms:
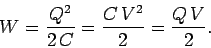 |
(120) |
These formulae are valid for any type of capacitor, since the arguments that we used
to derive them do not depend on any special property of parallel plate
capacitors.
Where is the energy in a parallel plate
capacitor actually stored? Well, if we think about
it, the only place it could be stored is in the electric field generated
between the plates. This insight allows us to calculate the energy (or, rather,
the energy density) of an electric field.
Consider a vacuum-filled parallel plate capacitor whose plates are of cross sectional area  ,
and are spaced a distance
,
and are spaced a distance  apart. The electric field
apart. The electric field 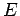 between the plates
is
approximately uniform, and of magnitude
between the plates
is
approximately uniform, and of magnitude
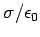 , where
, where 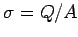 , and
, and 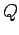 is the charge stored on the plates. The electric field elsewhere is approximately zero. The potential difference
between the plates is
is the charge stored on the plates. The electric field elsewhere is approximately zero. The potential difference
between the plates is 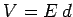 . Thus, the energy stored in the capacitor
can be written
. Thus, the energy stored in the capacitor
can be written
 |
(121) |
where use has been made of Eq. (108).
Now, 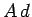 is the volume of the field-filled region between the plates, so if the
energy is stored in the electric field then the energy per unit volume,
or energy density, of the field must be
is the volume of the field-filled region between the plates, so if the
energy is stored in the electric field then the energy per unit volume,
or energy density, of the field must be
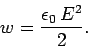 |
(122) |
It turns out that this result is quite general. Thus, we can calculate the energy
content of any electric field by dividing space into little cubes, applying the
above formula to find the energy content of each cube, and then summing the
energies thus obtained to obtain the total energy.
It is easily demonstrated that the energy density in a dielectric
medium is
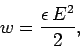 |
(123) |
where
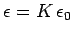 is the permittivity of the medium.
This energy density consists of two elements: the energy density
is the permittivity of the medium.
This energy density consists of two elements: the energy density
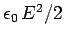 held in the electric field, and the energy density
held in the electric field, and the energy density
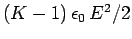 held in the dielectric medium (this represents the work done on the
constituent molecules of the dielectric
in order to polarize them).
held in the dielectric medium (this represents the work done on the
constituent molecules of the dielectric
in order to polarize them).



Next: Worked Examples
Up: Capacitance
Previous: Capacitors in Series and
Richard Fitzpatrick
2007-07-14
![]() and that the
potential difference between the plates is
and that the
potential difference between the plates is ![]() . The work we do in transferring
an infinitesimal amount of charge
. The work we do in transferring
an infinitesimal amount of charge ![]() from the negative to the
positive plate is simply
from the negative to the
positive plate is simply
![]() ,
and are spaced a distance
,
and are spaced a distance ![]() apart. The electric field
apart. The electric field ![]() between the plates
is
approximately uniform, and of magnitude
between the plates
is
approximately uniform, and of magnitude
![]() , where
, where ![]() , and
, and ![]() is the charge stored on the plates. The electric field elsewhere is approximately zero. The potential difference
between the plates is
is the charge stored on the plates. The electric field elsewhere is approximately zero. The potential difference
between the plates is ![]() . Thus, the energy stored in the capacitor
can be written
. Thus, the energy stored in the capacitor
can be written