


Next: Example 5.4: Electric potential due
Up: Electric Potential
Previous: Example 5.2: Motion of an
Question: A particle of charge
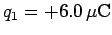 is located
on the
is located
on the  -axis at the point
-axis at the point
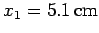 . A second particle of
charge
. A second particle of
charge
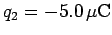 is placed on the
is placed on the  -axis at
-axis at
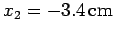 . What is
the absolute electric potential at the origin (
. What is
the absolute electric potential at the origin (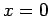 )? How much work must we perform in
order to slowly move a charge of
)? How much work must we perform in
order to slowly move a charge of
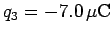 from infinity to the origin, whilst keeping
the other two charges fixed?
from infinity to the origin, whilst keeping
the other two charges fixed?
Solution: The absolute electric potential at the origin due to the first
charge is
Likewise, the absolute electric potential at the origin due to the second charge is
The net potential 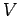 at the origin is simply the algebraic sum of the potentials due to each charge
taken in isolation. Thus,
at the origin is simply the algebraic sum of the potentials due to each charge
taken in isolation. Thus,
The work 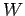 which we must perform in order to slowly moving a charge
which we must perform in order to slowly moving a charge 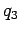 from infinity to the origin is
simply the product of the charge and the potential difference
from infinity to the origin is
simply the product of the charge and the potential difference 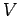 between the end and beginning
points. Thus,
between the end and beginning
points. Thus,



Next: Example 5.4: Electric potential due
Up: Electric Potential
Previous: Example 5.2: Motion of an
Richard Fitzpatrick
2007-07-14
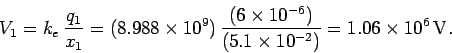
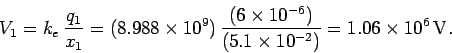
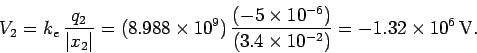
![]() which we must perform in order to slowly moving a charge
which we must perform in order to slowly moving a charge ![]() from infinity to the origin is
simply the product of the charge and the potential difference
from infinity to the origin is
simply the product of the charge and the potential difference ![]() between the end and beginning
points. Thus,
between the end and beginning
points. Thus,