


Next: Electric Field of a
Up: Gauss' Law
Previous: Gauss' Law
Electric Field of a Spherical Conducting Shell
Suppose that a thin, spherical, conducting shell carries a negative charge 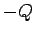 . We expect the
excess electrons to mutually repel one another, and, thereby, become uniformly distributed
over the surface of the shell. The electric field-lines produced outside such a
charge distribution point towards the surface of the conductor, and end on the
excess electrons. Moreover, the field-lines are normal to the surface of the conductor.
This must be the case, otherwise the electric field would have a component parallel
to the conducting surface. Since the excess electrons are free to move through the conductor,
any parallel component of the field would cause a redistribution of the charges
on the shell. This process will only cease when the parallel component
has been reduced to zero over the whole surface of the shell. It follows that:
. We expect the
excess electrons to mutually repel one another, and, thereby, become uniformly distributed
over the surface of the shell. The electric field-lines produced outside such a
charge distribution point towards the surface of the conductor, and end on the
excess electrons. Moreover, the field-lines are normal to the surface of the conductor.
This must be the case, otherwise the electric field would have a component parallel
to the conducting surface. Since the excess electrons are free to move through the conductor,
any parallel component of the field would cause a redistribution of the charges
on the shell. This process will only cease when the parallel component
has been reduced to zero over the whole surface of the shell. It follows that:
The electric field immediately above the surface of a conductor is directed
normal to that surface.
Figure 10:
The electric field generated by a negatively charged spherical
conducting shell.
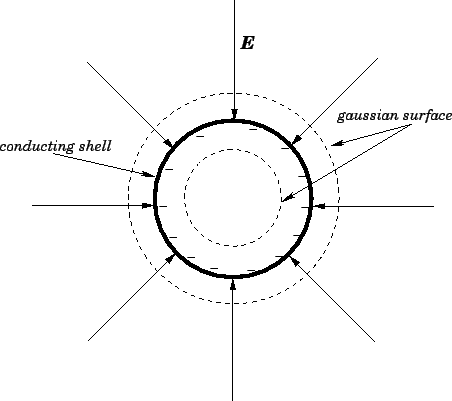 |
Let us consider an imaginary surface, usually referred to as a gaussian surface,
which is a sphere of radius 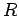 lying just above the surface of
the conductor. Since the electric field-lines are everywhere normal
to this surface, Gauss' law tells us that
lying just above the surface of
the conductor. Since the electric field-lines are everywhere normal
to this surface, Gauss' law tells us that
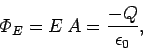 |
(68) |
where 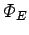 is the electric flux through the gaussian surface,
is the electric flux through the gaussian surface,
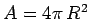 the area of this surface, and
the area of this surface, and 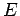 the electric
field-strength just above the surface of the conductor. Note that, by symmetry,
the electric
field-strength just above the surface of the conductor. Note that, by symmetry,
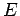 is
uniform over the surface of the conductor. It follows that
is
uniform over the surface of the conductor. It follows that
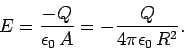 |
(69) |
But, this is the same result as would be obtained from Coulomb's law for
a point charge of magnitude 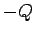 located at the centre of the conducting
shell. Now, a simple extension of the above argument leads to the conclusion that
Eq. (69) holds everywhere outside the shell (with
located at the centre of the conducting
shell. Now, a simple extension of the above argument leads to the conclusion that
Eq. (69) holds everywhere outside the shell (with 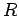 representing
the radial distance from the center of the shell).
Hence, we conclude the electric field outside a charged, spherical, conducting shell is the same as that generated when all the charge is concentrated at the centre of the shell.
representing
the radial distance from the center of the shell).
Hence, we conclude the electric field outside a charged, spherical, conducting shell is the same as that generated when all the charge is concentrated at the centre of the shell.
Let us repeat the above calculation using a spherical gaussian surface which
lies just inside the conducting shell. Now, the
gaussian surface encloses no charge, since all of the charge lies on the
shell, so it follows from Gauss' law, and symmetry, that the
electric field inside the shell is zero. In fact, the electric field inside
any closed
hollow conductor is zero (assuming that the region enclosed by the conductor
contains no charges).



Next: Electric Field of a
Up: Gauss' Law
Previous: Gauss' Law
Richard Fitzpatrick
2007-07-14

![]() lying just above the surface of
the conductor. Since the electric field-lines are everywhere normal
to this surface, Gauss' law tells us that
lying just above the surface of
the conductor. Since the electric field-lines are everywhere normal
to this surface, Gauss' law tells us that