


Next: Image Formation by Plane
Up: Paraxial Optics
Previous: Image Formation by Concave
The definitions of the principal axis, centre of curvature 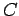 ,
radius of curvature
,
radius of curvature 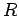 , and the vertex
, and the vertex  , of a convex mirror
are analogous to the corresponding definitions
for a concave mirror.
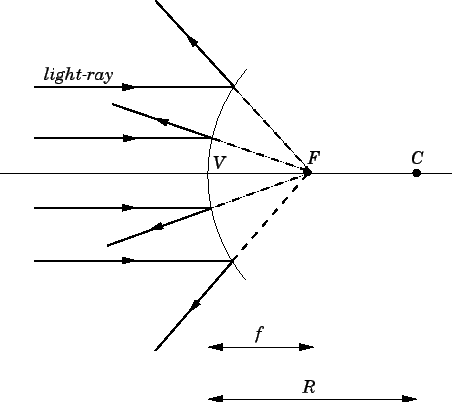
When parallel light-rays strike a convex mirror they are reflected
such that they appear to emanate from a single point
, of a convex mirror
are analogous to the corresponding definitions
for a concave mirror.
When parallel light-rays strike a convex mirror they are reflected
such that they appear to emanate from a single point 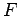 located behind the mirror, as shown in Fig. 74. This point is called the virtual focus
of the mirror. The focal length
located behind the mirror, as shown in Fig. 74. This point is called the virtual focus
of the mirror. The focal length
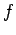 of the mirror is simply the distance between
of the mirror is simply the distance between  and
and 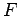 .
As is easily demonstrated, in the paraxial approximation, the focal length of a convex mirror
is half of its radius of curvature.
.
As is easily demonstrated, in the paraxial approximation, the focal length of a convex mirror
is half of its radius of curvature.
Figure 74:
The virtual focus of a convex mirror.
 |
There are, again, two alternative methods of locating the image
formed by a convex mirror. The first is graphical, and the second
analytical.
According to the graphical method,
the image produced by a convex mirror can always be located
by drawing a ray diagram according to four simple rules:
- An incident ray which is parallel to the principal axis
is reflected as if it came from the virtual focus
 of the
mirror.
of the
mirror.
- An incident ray which is directed towards the virtual
focus
 of the mirror is reflected parallel to the
principal axis.
of the mirror is reflected parallel to the
principal axis.
- An incident ray which is directed towards the centre of
curvature
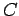 of the mirror is reflected back along its own
path (since it is normally incident on the mirror).
of the mirror is reflected back along its own
path (since it is normally incident on the mirror).
- An incident ray which strikes the mirror at its vertex
 is reflected such that its angle of incidence with respect to the
principal axis is equal to its angle of reflection.
is reflected such that its angle of incidence with respect to the
principal axis is equal to its angle of reflection.
The validity of these rules in the paraxial approximation is,
again, fairly self-evident.
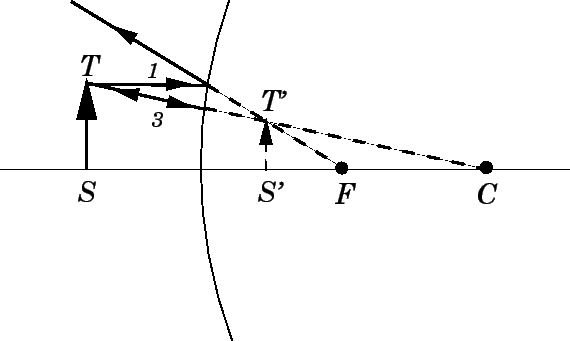
In the example shown in Fig. 75, two rays are used to locate the image
 of an object
of an object 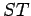 placed in front of the mirror.
It can be seen that the image is virtual, upright, and diminished.
placed in front of the mirror.
It can be seen that the image is virtual, upright, and diminished.
Figure 75:
Image formation by a convex mirror.
 |
As is easily demonstrated,
application of the analytical method to image formation by convex mirrors again
yields Eq. (352) for
the magnification of the image, and Eq. (358) for the location of the
image, provided that we adopt the following sign convention.
The focal length 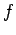 of a convex mirror is redefined to be minus the distance between points
of a convex mirror is redefined to be minus the distance between points  and
and 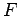 . In other words,
the focal length of a concave mirror, with a real focus, is always positive,
and the focal length of a convex mirror, with a virtual focus,
is always negative. Table 6
shows how the location and character of the image formed
in a convex spherical mirror depend on the location of
the object, according to Eqs. (352) and (358) (with
. In other words,
the focal length of a concave mirror, with a real focus, is always positive,
and the focal length of a convex mirror, with a virtual focus,
is always negative. Table 6
shows how the location and character of the image formed
in a convex spherical mirror depend on the location of
the object, according to Eqs. (352) and (358) (with 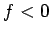 ).
).
Table 6:
Rules for image formation by convex mirrors.
| Position of object |
Position of image |
Character of image |
At 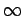 |
At 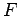 |
Virtual, zero size |
Between 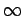 and and  |
Between 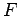 and and  |
Virtual, upright, diminished |
At  |
At  |
Virtual, upright, same size |
|
In summary, the formation of an image by a spherical mirror involves the
crossing of light-rays emitted by the object and reflected off
the mirror. If the light-rays actually cross in front of the
mirror then the image is real. If the light-rays do not
actually cross, but appear to cross when projected backwards
behind the mirror, then the image is virtual. A real image
can be projected onto a screen, a virtual image cannot.
However, both
types of images can be seen by an observer, and photographed by a
camera. The magnification of the image
is specified by Eq. (352), and the location of the image is determined
by
Eq. (358). These two formulae can be used to characterize both real
and virtual images formed by either concave or convex mirrors, provided
that the following sign conventions are observed:
- The height
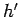 of the image is positive if the image is
upright, with respect to the object, and negative if the image
is inverted.
of the image is positive if the image is
upright, with respect to the object, and negative if the image
is inverted.
- The magnification
 of the image is positive if the image is
upright, with respect to the object, and negative if the image
is inverted.
of the image is positive if the image is
upright, with respect to the object, and negative if the image
is inverted.
- The image distance
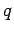 is positive if the image is real, and,
therefore, located in front of the mirror, and negative if the
image is virtual, and, therefore, located behind the mirror.
is positive if the image is real, and,
therefore, located in front of the mirror, and negative if the
image is virtual, and, therefore, located behind the mirror.
- The focal length
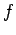 of
the mirror is positive if the mirror is concave, so that the focal
point
of
the mirror is positive if the mirror is concave, so that the focal
point 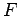 is located in front of
the mirror, and negative if the mirror is convex, so that the focal
point
is located in front of
the mirror, and negative if the mirror is convex, so that the focal
point 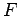 is located behind
the mirror.
is located behind
the mirror.
Note that the front side of the mirror is defined
to be the side from which the light is incident.



Next: Image Formation by Plane
Up: Paraxial Optics
Previous: Image Formation by Concave
Richard Fitzpatrick
2007-07-14

![]() of an object
of an object ![]() placed in front of the mirror.
It can be seen that the image is virtual, upright, and diminished.
placed in front of the mirror.
It can be seen that the image is virtual, upright, and diminished.
![]() of a convex mirror is redefined to be minus the distance between points
of a convex mirror is redefined to be minus the distance between points ![]() and
and ![]() . In other words,
the focal length of a concave mirror, with a real focus, is always positive,
and the focal length of a convex mirror, with a virtual focus,
is always negative. Table 6
shows how the location and character of the image formed
in a convex spherical mirror depend on the location of
the object, according to Eqs. (352) and (358) (with
. In other words,
the focal length of a concave mirror, with a real focus, is always positive,
and the focal length of a convex mirror, with a virtual focus,
is always negative. Table 6
shows how the location and character of the image formed
in a convex spherical mirror depend on the location of
the object, according to Eqs. (352) and (358) (with ![]() ).
).