Spherical Mirrors

A spherical mirror is a mirror which has the shape of a piece cut out of a spherical surface. There are two types of spherical mirrors: concave, and convex. These are illustrated in Fig. 68. The most commonly occurring examples of concave mirrors are shaving mirrors and makeup mirrors. As is well-known, these types of mirrors magnify objects placed close to them. The most commonly occurring examples of convex mirrors are the passenger-side wing mirrors of cars. These type of mirrors have wider fields of view than equivalent flat mirrors, but objects which appear in them generally look smaller (and, therefore, farther away) than they actually are.

Figure 68: A concave (left) and a convex (right) mirror

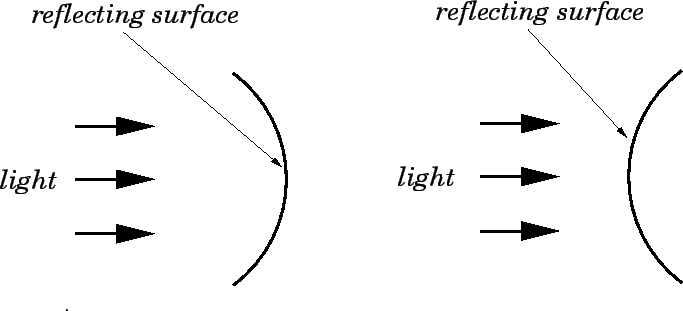
Let us now introduce a few key concepts which are needed to study image formation by a concave spherical mirror. As illustrated in Fig. 69, the normal to the centre of the mirror is called the principal axis. The mirror is assumed to be rotationally symmetric about this axis. Hence, we can represent a three-dimensional mirror in a two-dimensional diagram, without loss of generality. The point $V$ at which the principal axis touches the surface of the mirror is called the vertex. The point $C$, on the principal axis, which is equidistant from all points on the reflecting surface of the mirror is called the centre of curvature. The distance along the principal axis from point $C$ to point $V$ is called the radius of curvature of the mirror, and is denoted $R$. It is found experimentally that rays striking a concave mirror parallel to its principal axis, and not too far away from this axis, are reflected by the mirror such that they all pass through the same point $F$ on the principal axis. This point, which is lies between the centre of curvature and the vertex, is called the focal point, or focus, of the mirror. The distance along the principal axis from the focus to the vertex is called the focal length of the mirror, and is denoted $f$.

Figure 69: Image formation by a concave mirror.

In our study of concave mirrors, we are going to assume that all light-rays which strike a mirror parallel to its principal axis (e.g., all rays emanating from a distant object) are brought to a focus at the same point $F$. Of course, as mentioned above, this is only an approximation. It turns out that as rays from a distant object depart further from the principal axis of a concave mirror they are brought to a focus ever closer to the mirror, as shown in Fig. 70. This lack of perfect focusing of a spherical mirror is called spherical aberration. The approximation in which we neglect spherical aberration is called the paraxial approximation.³ Likewise, the study of image formation under this approximation is known as paraxial optics. This field of optics was first investigated systematically by the famous German mathematician Karl Friedrich Gauss in 1841.

Figure 70: Spherical aberration in a concave mirror.

It can be demonstrated, by geometry, that the only type of mirror which does not suffer from spherical aberration is a parabolic mirror (i.e., a mirror whose reflecting surface is the surface of revolution of a parabola). Thus, a ray traveling parallel to the principal axis of a parabolic mirror is brought to a focus at the same point $F$, no matter how far the ray is from the axis. Since the path of a light-ray is completely reversible, it follows that a light source placed at the focus $F$ of a parabolic mirror yields a perfectly parallel beam of light, after the light has reflected off the surface of the mirror. Parabolic mirrors are more difficult, and, therefore, more expensive, to make than spherical mirrors. Thus, parabolic mirrors are only used in situations where the spherical aberration of a conventional spherical mirror would be a serious problem. The receiving dishes of radio telescopes are generally parabolic. They reflect the incoming radio waves from (very) distant astronomical sources, and bring them to a focus at a single point, where a detector is placed. In this case, since the sources are extremely faint, it is imperative to avoid the signal losses which would be associated with spherical aberration. A car headlight consists of a light-bulb placed at the focus of a parabolic reflector. The use of a parabolic reflector enables the headlight to cast a very straight beam of light ahead of the car. The beam would be nowhere near as well-focused were a spherical reflector used instead.