Rainbows

The most well-known, naturally occurring phenomenon which involves the dispersion of light is a rainbow. A rainbow is an arc of light, with an angular radius of $42^\circ$, centred on a direction which is opposite to that of the Sun in the sky (i.e., it is centred on the direction of propagation of the Sun's rays)--see Fig. 65. Thus, if the Sun is low in the sky (i.e., close to the horizon) we see almost a full semi-circle. If the Sun is higher in the sky we see a smaller arc, and if the Sun is more than $42^\circ$ above the horizon then there is no rainbow (for viewers on the Earth's surface). Observers on a hill may see parts of the rainbow below the horizontal: i.e., an arc greater than a semi-circle. Passengers on an airplane can sometimes see a full circle.

Figure 65: A rainbow.

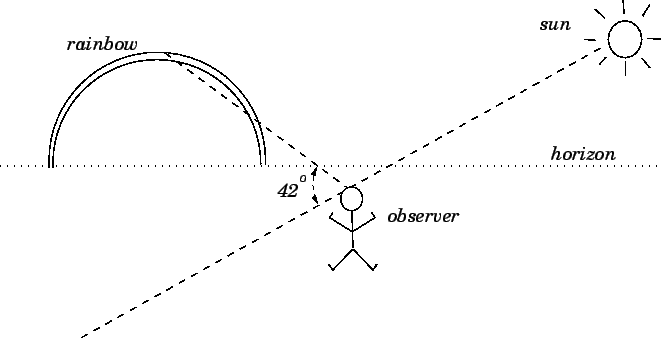
The colours of a rainbow vary smoothly from red on the outside of the arc to violet on the inside. A rainbow has a diffuse inner edge, and a sharp outer edge. Sometimes a secondary arc is observed. This is fainter and larger (with an angular radius of $50^\circ$) than the primary arc, and the order of the colours is reversed (i.e., red is on the inside, and violet on the outside). The secondary arc has a diffuse outer edge, and a sharp inner edge. The sky between the two arcs sometimes appears to be less bright than the sky elsewhere. This region is called Alexander's dark band, in honour of Alexander of Aphrodisias who described it some 1800 years ago.

Rainbows have been studied since ancient times. Aristotle wrote extensively on rainbows in his De Meteorologica,² and even speculated that a rainbow is caused by the reflection of sunlight from the drops of water in a cloud.

The first scientific study of rainbows was performed by Theodoric, professor of theology at Freiburg, in the fourteenth century. He studied the path of a light-ray through a spherical globe of water in his laboratory, and suggested that the globe be thought of as a model of a single falling raindrop. A ray, from the Sun, entering the drop, is refracted at the air-water interface, undergoes internal reflection from the inside surface of the drop, and then leaves the drop in a backward direction, after being again refracted at the surface. Thus, looking away from the Sun, towards a cloud of raindrops, one sees an enhancement of light due to these rays. Theodoric did not explain why this enhancement is concentrated at a particular angle from the direction of the Sun's rays, or why the light is split into different colours.

The first person to give a full explanation of how a rainbow is formed was René Descartes. He showed mathematically that if one traces the path through a spherical raindrop of parallel light-rays entering the drop at different points on its surface, each emerges in a different direction, but there is a concentration of emerging rays at an angle of $42^\circ$ from the reverse direction to the incident rays, in exact agreement with the observed angular size of rainbows. Furthermore, since some colours are refracted more than others in a raindrop, the ``rainbow angle'' is slightly different for each colour, so a raindrop disperses the Sun's light into a set of nearly overlapping coloured arcs.

Figure 65 illustrated Descartes' theory in more detail. It shows parallel light-rays entering a spherical raindrop. Only rays entering the upper half contribute to the rainbow effect. Let us follow the rays, one by one, from the top down to the middle of the drop. We observe the following pattern. Rays which enter near the top of the drop emerge going in almost the reverse direction, but a few degrees below the horizontal. Rays entering a little further below the top emerge at a greater angle below the horizontal. Eventually, we reach a critical ray, called the rainbow ray, which emerges in an angle $42^\circ$ below the horizontal. Rays entering the drop lower than the rainbow ray emerge at an angle less than $42^\circ$. Thus, the rainbow ray is the one which deviates most from the reverse direction to the incident rays. This variation, with $42^\circ$ being the maximum angle of deviation from the reverse direction, leads to a bunching of rays at that angle, and, hence, to an unusually bright arc of reflected light centred around $42^\circ$ from the reverse direction. The arc has a sharp outer edge, since reflected light cannot deviate by more than $42^\circ$ from the reverse direction, and a diffuse inner edge, since light can deviate by less than $42^\circ$ from the reverse direction: $42^\circ$ is just the most likely angle of deviation. Finally, since the rainbow angle varies slightly with wavelength (because the refractive index of water varies slightly with wavelength), the arcs corresponding to each colour appear at slightly different angles relative to the reverse direction to the incident rays. We expect violet light to be refracted more strongly than red light in a raindrop. It is, therefore, clear, from Fig. 66, that the red arc deviates slightly more from the reverse direction to the incident rays than the violet arc. In other words, violet is concentrated on the inside of the rainbow, and red is concentrated on the outside.

Figure 66: Descarte's theory of the rainbow.

Descartes was also able to show that light-rays which are internally reflected twice inside a raindrop emerge concentrated at an angle of $50^\circ$ from the reverse direction to the incident rays. Of course, this angle corresponds exactly to the angular size of the secondary rainbow sometimes seen outside the first. This rainbow is naturally less intense than the primary rainbow, since a light-ray loses some of its intensity at each reflection or refraction event. Note that $50^\circ$ represents the angle of maximum deviation of doubly reflected light from the reverse direction (i.e., doubly reflected light can deviate by more than this angle, but not by less). Thus, we expect the secondary rainbow to have a diffuse outer edge, and a sharp inner edge. We also expect doubly reflected violet light to be refracted more strongly in a raindrop than doubly reflected red light. It follows, from Fig. 67, that the red secondary arc deviates slightly less from the reverse direction to the incident rays than the violet secondary arc. In other words, red is concentrated on the inside of the secondary rainbow, and violet on the outside. Since no reflected light emerges between the primary and secondary rainbows (i.e., in the angular range $42^\circ$ to $50^\circ$, relative to the reverse direction), we naturally expect this region of the sky to look slightly less bright than the other surrounding regions of the sky, which explains Alexander's dark band.

Figure 67: Rainbow rays for the primary and secondary arcs of a rainbow.