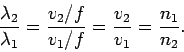Next: Total Internal Reflection
Up: Geometric Optics
Previous: Law of Reflection
The law of refraction, which is generally
known as Snell's law, governs the behaviour of light-rays as
they propagate across a sharp interface between two
transparent dielectric media.
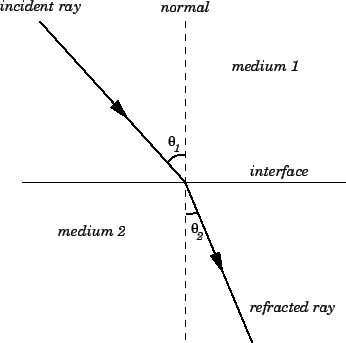
Consider a light-ray incident on a plane interface between two
transparent dielectric media, labelled 1 and 2, as shown in Fig. 57.
The law of refraction states that the incident ray, the refracted ray,
and the normal to the interface, all lie in the same plane.
Furthermore,
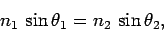 |
(341) |
where 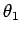 is the angle subtended between the incident ray and
the normal to the interface, and
is the angle subtended between the incident ray and
the normal to the interface, and 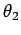 is the angle subtended between the
refracted ray and the normal to the
interface. The quantities
is the angle subtended between the
refracted ray and the normal to the
interface. The quantities 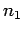 and
and 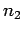 are
termed the refractive indices of media 1 and 2, respectively.
Thus, the law of refraction predicts that a light-ray always
deviates more towards
the normal in the optically denser medium: i.e.,
the medium with the higher refractive index. Note that
are
termed the refractive indices of media 1 and 2, respectively.
Thus, the law of refraction predicts that a light-ray always
deviates more towards
the normal in the optically denser medium: i.e.,
the medium with the higher refractive index. Note that  in the figure. The law of refraction also holds for non-planar
interfaces, provided that the normal to the interface at any given point
is understood to be the normal to the local tangent plane of the
interface at that
point.
in the figure. The law of refraction also holds for non-planar
interfaces, provided that the normal to the interface at any given point
is understood to be the normal to the local tangent plane of the
interface at that
point.
Figure 57:
The law of refraction.
 |
By definition, the refractive index 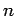 of a dielectric medium
of dielectric constant
of a dielectric medium
of dielectric constant 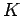 is given by
is given by
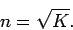 |
(342) |
Table 4 shows the refractive indices of some common
materials (for yellow light of wavelength 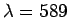 nm).
nm).
Table 4:
Refractive indices of some common materials at 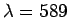 nm.
nm.
| Material |
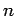 |
| Air (STP) |
1.00029 |
| Water |
1.33 |
| Ice |
1.31 |
| Glass: |
|
| Light flint |
1.58 |
| Heavy flint |
1.65 |
| Heaviest flint |
1.89 |
| Diamond |
2.42 |
|
The law of refraction follows directly from the fact that
the speed  with which light propagates through a dielectric medium
is inversely proportional to the refractive index of the
medium (see Sect. 11.3). In fact,
with which light propagates through a dielectric medium
is inversely proportional to the refractive index of the
medium (see Sect. 11.3). In fact,
 |
(343) |
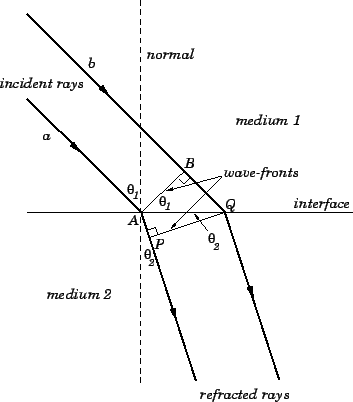
where 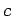 is the speed of light in a vacuum. Consider two
parallel light-rays,
is the speed of light in a vacuum. Consider two
parallel light-rays, 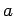 and
and 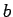 , incident at an angle
, incident at an angle 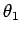 with
respect to the normal to the interface between two dielectric media,
1 and 2. Let the refractive indices of the two media be
with
respect to the normal to the interface between two dielectric media,
1 and 2. Let the refractive indices of the two media be 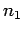 and
and
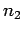 respectively, with
respectively, with 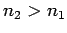 . It is clear from Fig. 58
that ray
. It is clear from Fig. 58
that ray 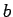 must move from point
must move from point
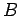 to point
to point 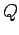 , in medium 1, in the same time interval,
, in medium 1, in the same time interval,
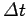 , in which
ray
, in which
ray 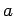 moves between points
moves between points  and
and 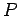 , in medium 2. Now, the
speed of light in medium 1 is
, in medium 2. Now, the
speed of light in medium 1 is  , whereas the speed
of light in medium 2 is
, whereas the speed
of light in medium 2 is 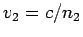 . It follows that the
length
. It follows that the
length 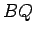 is given by
is given by
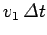 , whereas the
length
, whereas the
length 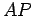 is given by
is given by
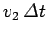 . By trigonometry,
. By trigonometry,
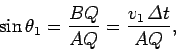 |
(344) |
and
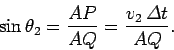 |
(345) |
Hence,
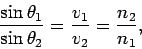 |
(346) |
which can be rearranged to give Snell's law. Note that the
lines 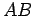 and
and  represent wave-fronts in media 1 and 2, respectively, and,
therefore, cross rays
represent wave-fronts in media 1 and 2, respectively, and,
therefore, cross rays 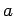 and
and 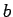 at right-angles.
at right-angles.
Figure 58:
Derivation of Snell's law.
 |
When light passes from one dielectric medium to another
its velocity  changes, but its frequency
changes, but its frequency 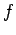 remains unchanged.
Since,
remains unchanged.
Since, 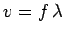 for all waves, where
for all waves, where 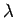 is the wavelength,
it follows that the wavelength of light must also change as it crosses
an interface between two different media.
Suppose that light propagates
from medium 1 to medium 2. Let
is the wavelength,
it follows that the wavelength of light must also change as it crosses
an interface between two different media.
Suppose that light propagates
from medium 1 to medium 2. Let 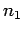 and
and 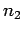 be the refractive
indices of the two media, respectively. The ratio of the
wave-lengths in the two media is given by
be the refractive
indices of the two media, respectively. The ratio of the
wave-lengths in the two media is given by
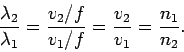 |
(347) |
Thus, as light moves from air to glass its
wavelength decreases.



Next: Total Internal Reflection
Up: Geometric Optics
Previous: Law of Reflection
Richard Fitzpatrick
2007-07-14
![]() of a dielectric medium
of dielectric constant
of a dielectric medium
of dielectric constant ![]() is given by
is given by
![]() with which light propagates through a dielectric medium
is inversely proportional to the refractive index of the
medium (see Sect. 11.3). In fact,
with which light propagates through a dielectric medium
is inversely proportional to the refractive index of the
medium (see Sect. 11.3). In fact,
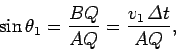
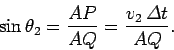
![]() changes, but its frequency
changes, but its frequency ![]() remains unchanged.
Since,
remains unchanged.
Since, ![]() for all waves, where
for all waves, where ![]() is the wavelength,
it follows that the wavelength of light must also change as it crosses
an interface between two different media.
Suppose that light propagates
from medium 1 to medium 2. Let
is the wavelength,
it follows that the wavelength of light must also change as it crosses
an interface between two different media.
Suppose that light propagates
from medium 1 to medium 2. Let ![]() and
and ![]() be the refractive
indices of the two media, respectively. The ratio of the
wave-lengths in the two media is given by
be the refractive
indices of the two media, respectively. The ratio of the
wave-lengths in the two media is given by