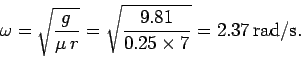Next: Worked example 7.4: Aerobatic
Up: Circular motion
Previous: Worked example 7.2: Circular
Question: An amusement park ride consists of a vertical cylinder that
spins about a vertical axis. When the cylinder spins sufficiently fast, any person
inside it is held up against the wall. Suppose that the coefficient of static
friction between a typical person and the wall is 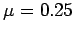 . Let the mass of an typical
person be
. Let the mass of an typical
person be
 , and let
, and let 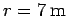 be the radius of the cylinder.
Find the critical angular velocity of the cylinder above which a typical person
will not slide down the wall. How many revolutions per second
is the cylinder executing at this critical velocity?
be the radius of the cylinder.
Find the critical angular velocity of the cylinder above which a typical person
will not slide down the wall. How many revolutions per second
is the cylinder executing at this critical velocity?
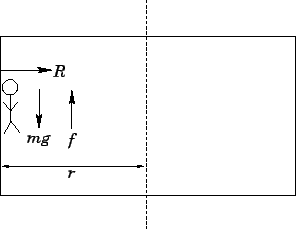
Answer: In the vertical direction, the person is subject to
a downward force  due to gravity, and a maximum upward force
due to gravity, and a maximum upward force 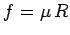 due
to friction with the wall. Here,
due
to friction with the wall. Here,  is the normal reaction between the person
and the wall. In order for the person not to slide down the wall, we require
is the normal reaction between the person
and the wall. In order for the person not to slide down the wall, we require
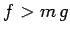 . Hence, the critical case corresponds to
. Hence, the critical case corresponds to
In the radial direction, the person is subject to a single force: namely, the reaction
 due to the wall, which acts radially inwards. If the cylinder (and, hence, the person)
rotates with angular velocity
due to the wall, which acts radially inwards. If the cylinder (and, hence, the person)
rotates with angular velocity  , then this force must provided the acceleration
, then this force must provided the acceleration
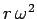 towards the axis of rotation. Hence,
towards the axis of rotation. Hence,
It follows that, in the critical case,
The corresponding number of revolutions per second is



Next: Worked example 7.4: Aerobatic
Up: Circular motion
Previous: Worked example 7.2: Circular
Richard Fitzpatrick
2006-02-02

![]() due to gravity, and a maximum upward force
due to gravity, and a maximum upward force ![]() due
to friction with the wall. Here,
due
to friction with the wall. Here, ![]() is the normal reaction between the person
and the wall. In order for the person not to slide down the wall, we require
is the normal reaction between the person
and the wall. In order for the person not to slide down the wall, we require
![]() . Hence, the critical case corresponds to
. Hence, the critical case corresponds to
![]() due to the wall, which acts radially inwards. If the cylinder (and, hence, the person)
rotates with angular velocity
due to the wall, which acts radially inwards. If the cylinder (and, hence, the person)
rotates with angular velocity ![]() , then this force must provided the acceleration
, then this force must provided the acceleration
![]() towards the axis of rotation. Hence,
towards the axis of rotation. Hence,