Next: Conservation of momentum
Up: Conservation of energy
Previous: Worked example 5.5: Sliding
Question: A car of weight 3000N possesses an engine whose maximum
power output is 160kW. The maximum speed of this car on a
level road is 35m/s. Assuming that the
resistive force (due to a combination of friction and
air resistance) remains constant, what is the car's maximum
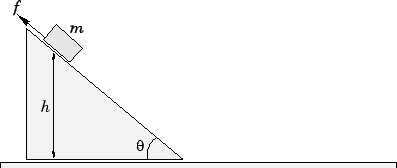
speed on an incline of 1 in 20 (i.e., if  is the angle of the incline with respect to the horizontal, then
is the angle of the incline with respect to the horizontal, then
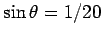 )?
)?
Answer:
When the car is traveling on a level road at its maximum speed,  , then all
of the power output,
, then all
of the power output, 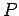 , of its engine is used to overcome the power
dissipated by the resistive force,
, of its engine is used to overcome the power
dissipated by the resistive force, 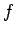 . Hence,
. Hence,
where the left-hand side is the power output of the engine, and the right-hand side
is the power dissipated by the resistive force (i.e., minus the rate at which
this force does work on the car). It follows that
When the car, whose weight is 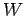 , is traveling up an incline, whose angle with respect
to the horizontal is
, is traveling up an incline, whose angle with respect
to the horizontal is  , it is subject to the additional
force
, it is subject to the additional
force
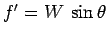 , which acts to impede its motion.
Of course, this force is
just the component of the car's weight acting down the incline. Thus, the
new power balance equation is written
, which acts to impede its motion.
Of course, this force is
just the component of the car's weight acting down the incline. Thus, the
new power balance equation is written
where 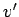 is the maximum velocity of the car up the incline. Here, the
left-hand side represents the power output of the car, whereas the right-hand
side represents the sum of the power dissipated by the resistive force and the power expended to
overcome the component of the car's weight acting down the incline. It follows that
is the maximum velocity of the car up the incline. Here, the
left-hand side represents the power output of the car, whereas the right-hand
side represents the sum of the power dissipated by the resistive force and the power expended to
overcome the component of the car's weight acting down the incline. It follows that



Next: Conservation of momentum
Up: Conservation of energy
Previous: Worked example 5.5: Sliding
Richard Fitzpatrick
2006-02-02
![]() , then all
of the power output,
, then all
of the power output, ![]() , of its engine is used to overcome the power
dissipated by the resistive force,
, of its engine is used to overcome the power
dissipated by the resistive force, ![]() . Hence,
. Hence,
![]() , is traveling up an incline, whose angle with respect
to the horizontal is
, is traveling up an incline, whose angle with respect
to the horizontal is ![]() , it is subject to the additional
force
, it is subject to the additional
force
![]() , which acts to impede its motion.
Of course, this force is
just the component of the car's weight acting down the incline. Thus, the
new power balance equation is written
, which acts to impede its motion.
Of course, this force is
just the component of the car's weight acting down the incline. Thus, the
new power balance equation is written