


Next: Worked example 4.1: In
Up: Newton's laws of motion
Previous: Friction
Frames of reference
As discussed in Sect. 1, the laws of physics are assumed to possess objective reality.
In other words, it is assumed that two independent observers, studying the same physical phenomenon,
would eventually formulate identical laws of physics in order to account for their
observations. Now, two completely independent observers are likely to choose different systems of units
with which to quantify physical measurements. However, as we have seen in Sect. 1, the
dimensional consistency of valid laws of physics renders them invariant under transformation from
one system of units to another. Independent observers are also likely to choose
different coordinate systems. For instance, the origins of their separate coordinate systems might
differ, as well as the orientation of the various coordinate axes. Are the laws of physics also
invariant under transformation between coordinate systems possessing different origins,
or a different orientation of the various coordinate axes?
Consider the vector equation
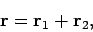 |
(116) |
which is represented diagrammatically in Fig. 12. Suppose that we shift the origin
of our coordinate system, or rotate the coordinate axes. Clearly, in general, the components
of vectors  ,
, 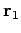 , and
, and 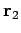 are going to be modified by this change
in our coordinate scheme.
However, Fig. 12 still remains valid. Hence, we conclude that the vector
equation (116) also remains valid. In other words, although the individual
components of vectors
are going to be modified by this change
in our coordinate scheme.
However, Fig. 12 still remains valid. Hence, we conclude that the vector
equation (116) also remains valid. In other words, although the individual
components of vectors  ,
, 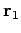 , and
, and 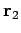 are modified by the change in
coordinate scheme, the interrelation between these components expressed in Eq. (116) remains
invariant.
This observation suggests that the independence of the laws of
physics from the arbitrary choice of the location of the underlying coordinate system's origin,
or the equally arbitrary choice of the orientation of the various coordinate axes, can be made
manifest by simply writing these laws as interrelations between vectors.
In particular, Newton's second law of motion,
are modified by the change in
coordinate scheme, the interrelation between these components expressed in Eq. (116) remains
invariant.
This observation suggests that the independence of the laws of
physics from the arbitrary choice of the location of the underlying coordinate system's origin,
or the equally arbitrary choice of the orientation of the various coordinate axes, can be made
manifest by simply writing these laws as interrelations between vectors.
In particular, Newton's second law of motion,
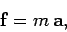 |
(117) |
is clearly invariant under shifts in the origin of our coordinate system, or changes
in the orientation of the various coordinate axes. Note that the quantity  (i.e., the mass of the body whose motion is under investigation),
appearing in the above equation, is invariant under any changes in the coordinate
system, since measurements
of mass are completely independent of measurements of distance. We refer to
such a quantity as a scalar (this is an improved definition).
We conclude that valid laws
of physics must consist of combinations of scalars and vectors, otherwise
they would retain an unphysical dependence on the details of the chosen coordinate system.
(i.e., the mass of the body whose motion is under investigation),
appearing in the above equation, is invariant under any changes in the coordinate
system, since measurements
of mass are completely independent of measurements of distance. We refer to
such a quantity as a scalar (this is an improved definition).
We conclude that valid laws
of physics must consist of combinations of scalars and vectors, otherwise
they would retain an unphysical dependence on the details of the chosen coordinate system.
Up to now, we have implicitly assumed that all of our observers are stationary
(i.e., they are all standing still on the surface of the Earth). Let us, now,
relax this assumption. Consider two observers,  and
and 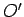 , whose coordinate systems
coincide momentarily at
, whose coordinate systems
coincide momentarily at  . Suppose that observer
. Suppose that observer  is stationary (on the surface of the
Earth), whereas observer
is stationary (on the surface of the
Earth), whereas observer 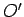 moves (with respect to observer
moves (with respect to observer  ) with
uniform velocity
) with
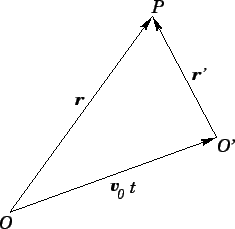
uniform velocity  . As illustrated in Fig. 34, if
. As illustrated in Fig. 34, if  represents
the displacement of some body
represents
the displacement of some body 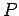 in the stationary observer's frame of reference, at time
in the stationary observer's frame of reference, at time  , then
the corresponding displacement in the moving observer's frame of reference is simply
, then
the corresponding displacement in the moving observer's frame of reference is simply
 |
(118) |
The velocity of body 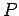 in the stationary observer's frame of reference is defined as
in the stationary observer's frame of reference is defined as
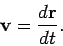 |
(119) |
Hence, the corresponding velocity in the moving observer's frame of reference takes the form
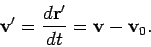 |
(120) |
Finally, the acceleration of body 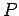 in stationary observer's frame of reference is
defined as
in stationary observer's frame of reference is
defined as
 |
(121) |
whereas the corresponding acceleration in the moving observer's frame of reference takes the form
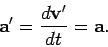 |
(122) |
Hence, the acceleration of body 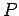 is identical in both frames of reference.
is identical in both frames of reference.
Figure 34:
A moving observer
 |
It is clear that if observer  concludes that body
concludes that body 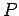 is moving with constant
velocity, and, therefore, subject to zero net force, then observer
is moving with constant
velocity, and, therefore, subject to zero net force, then observer 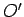 will agree
with this conclusion. Furthermore, if observer
will agree
with this conclusion. Furthermore, if observer  concludes that body
concludes that body 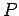 is accelerating, and, therefore, subject to a force
is accelerating, and, therefore, subject to a force 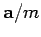 , then observer
, then observer
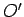 will remain in agreement. It follows that Newton's laws of motion
are equally valid in the frames of reference of the moving and the stationary observer.
Such frames are termed inertial frames of reference. There are infinitely many
inertial frames of reference--within which Newton's laws of motion are equally valid--all
moving with constant velocity with respect to one another. Consequently, there is no universal
standard of rest in physics. Observer
will remain in agreement. It follows that Newton's laws of motion
are equally valid in the frames of reference of the moving and the stationary observer.
Such frames are termed inertial frames of reference. There are infinitely many
inertial frames of reference--within which Newton's laws of motion are equally valid--all
moving with constant velocity with respect to one another. Consequently, there is no universal
standard of rest in physics. Observer  might claim to be at rest compared to observer
might claim to be at rest compared to observer 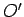 ,
and vice versa: however, both points of view are equally valid. Moreover, there is
absolutely no physical
experiment which observer
,
and vice versa: however, both points of view are equally valid. Moreover, there is
absolutely no physical
experiment which observer  could perform in order to demonstrate that he/she is at
rest whilst observer
could perform in order to demonstrate that he/she is at
rest whilst observer 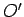 is moving. This, in essence, is the principle of special
relativity, first formulated by Albert Einstein in 1905.
is moving. This, in essence, is the principle of special
relativity, first formulated by Albert Einstein in 1905.



Next: Worked example 4.1: In
Up: Newton's laws of motion
Previous: Friction
Richard Fitzpatrick
2006-02-02
![]() and
and ![]() , whose coordinate systems
coincide momentarily at
, whose coordinate systems
coincide momentarily at ![]() . Suppose that observer
. Suppose that observer ![]() is stationary (on the surface of the
Earth), whereas observer
is stationary (on the surface of the
Earth), whereas observer ![]() moves (with respect to observer
moves (with respect to observer ![]() ) with
uniform velocity
) with
uniform velocity ![]() . As illustrated in Fig. 34, if
. As illustrated in Fig. 34, if ![]() represents
the displacement of some body
represents
the displacement of some body ![]() in the stationary observer's frame of reference, at time
in the stationary observer's frame of reference, at time ![]() , then
the corresponding displacement in the moving observer's frame of reference is simply
, then
the corresponding displacement in the moving observer's frame of reference is simply
![]() concludes that body
concludes that body ![]() is moving with constant
velocity, and, therefore, subject to zero net force, then observer
is moving with constant
velocity, and, therefore, subject to zero net force, then observer ![]() will agree
with this conclusion. Furthermore, if observer
will agree
with this conclusion. Furthermore, if observer ![]() concludes that body
concludes that body ![]() is accelerating, and, therefore, subject to a force
is accelerating, and, therefore, subject to a force ![]() , then observer
, then observer
![]() will remain in agreement. It follows that Newton's laws of motion
are equally valid in the frames of reference of the moving and the stationary observer.
Such frames are termed inertial frames of reference. There are infinitely many
inertial frames of reference--within which Newton's laws of motion are equally valid--all
moving with constant velocity with respect to one another. Consequently, there is no universal
standard of rest in physics. Observer
will remain in agreement. It follows that Newton's laws of motion
are equally valid in the frames of reference of the moving and the stationary observer.
Such frames are termed inertial frames of reference. There are infinitely many
inertial frames of reference--within which Newton's laws of motion are equally valid--all
moving with constant velocity with respect to one another. Consequently, there is no universal
standard of rest in physics. Observer ![]() might claim to be at rest compared to observer
might claim to be at rest compared to observer ![]() ,
and vice versa: however, both points of view are equally valid. Moreover, there is
absolutely no physical
experiment which observer
,
and vice versa: however, both points of view are equally valid. Moreover, there is
absolutely no physical
experiment which observer ![]() could perform in order to demonstrate that he/she is at
rest whilst observer
could perform in order to demonstrate that he/she is at
rest whilst observer ![]() is moving. This, in essence, is the principle of special
relativity, first formulated by Albert Einstein in 1905.
is moving. This, in essence, is the principle of special
relativity, first formulated by Albert Einstein in 1905.