Hooke's law

One method of quantifying the force exerted on an object is via Hooke's law. This law--discovered by the English scientist Robert Hooke in 1660--states that the force $f$ exerted by a coiled spring is directly proportional to its extension ${\mit\Delta} x$. The extension of the spring is the difference between its actual length and its natural length (i.e., its length when it is exerting no force). The force acts parallel to the axis of the spring. Obviously, Hooke's law only holds if the extension of the spring is sufficiently small. If the extension becomes too large then the spring deforms permanently, or even breaks. Such behaviour lies beyond the scope of Hooke's law.

Figure 21: Hooke's law

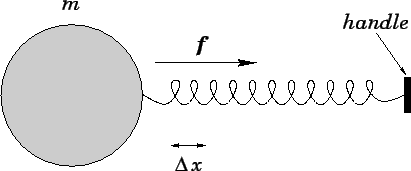
Figure 21 illustrates how we might use Hooke's law to quantify the force we exert on a body of mass $m$ when we pull on the handle of a spring attached to it. The magnitude $f$ of the force is proportional to the extension of the spring: twice the extension means twice the force. As shown, the direction of the force is towards the spring, parallel to its axis (assuming that the extension is positive). The magnitude of the force can be quantified in terms of the critical extension required to impart a unit acceleration (i.e., $1 {\rm m/s^2}$) to a body of unit mass (i.e., $1 {\rm kg}$). According to Eq. (94), the force corresponding to this extension is 1 newton. Here, a newton (symbol N) is equivalent to a kilogram-meter per second-squared, and is the mks unit of force. Thus, if the critical extension corresponds to a force of $1 {\rm N}$ then half the critical extension corresponds to a force of $0.5 {\rm N}$, and so on. In this manner, we can quantify both the direction and magnitude of the force we exert, by means of a spring, on a given body.

Suppose that we apply two forces, ${\bf f}_1$ and ${\bf f}_2$ (say), acting in different directions, to a body of mass $m$ by means of two springs. As illustrated in Fig. 22, the body accelerates as if it were subject to a single force ${\bf f}$ which is the vector sum of the individual forces ${\bf f}_1$ and ${\bf f}_2$. It follows that the force ${\bf f}$ appearing in Newton's second law of motion, Eq. (94), is the resultant of all the external forces to which the body whose motion is under investigation is subject.

Figure 22: Addition of forces

Suppose that the resultant of all the forces acting on a given body is zero. In other words, suppose that the forces acting on the body exactly balance one another. According to Newton's second law of motion, Eq. (94), the body does not accelerate: i.e., it either remains at rest or moves with uniform velocity in a straight line. It follows that Newton's first law of motion applies not only to bodies which have no forces acting upon them but also to bodies acted upon by exactly balanced forces.