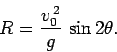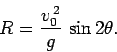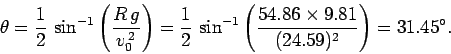Next: Worked example 3.5: Flight
Up: Motion in 3 dimensions
Previous: Worked example 3.3: Cannon
Question: The Longhorns are down by 4 points with 5s left in the
fourth quarter. Chris Simms launches a Hail Mary pass into the end-zone,
60 yards away, where B.J. Johnson is waiting to make the catch. Suppose
that Chris throws the ball at 55 miles per hour. At what angle to the horizontal
must the ball be launched in order for it to hit the receiver? Neglect the effect of air resistance.
Answer: The formula for the horizontal range  of a projectile thrown
with initial velocity
of a projectile thrown
with initial velocity 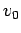 at an angle
at an angle  to the horizontal is [see
Eq. (77)]:
to the horizontal is [see
Eq. (77)]:
In this case,
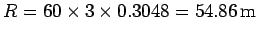 and
and
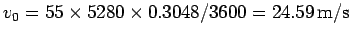 . Hence,
. Hence,
Thus, the ball must be launched at 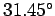 to the horizontal. (Actually,
to the horizontal. (Actually,
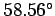 would work just as well. Why is this?)
would work just as well. Why is this?)
Richard Fitzpatrick
2006-02-02