Vector displacement

Consider the motion of a body moving in 3 dimensions. The body's instantaneous position is most conveniently specified by giving its displacement from the origin of our coordinate system. Note, however, that in 3 dimensions such a displacement possesses both magnitude and direction. In other words, we not only have to specify how far the body is situated from the origin, we also have to specify in which direction it lies. A quantity which possesses both magnitude and direction is termed a vector. By contrast, a quantity which possesses only magnitude is termed a scalar. Mass and time are scalar quantities. However, in general, displacement is a vector.

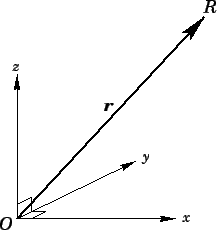
The vector displacement ${\bf r}$ of some point $R$ from the origin $O$ can be visualized as an arrow running from point $O$ to point $R$. See Fig. 11. Note that in typeset documents vector quantities are conventionally written in a bold-faced font (e.g., ${\bf r}$) to distinguish them from scalar quantities. In free-hand notation, vectors are usually under-lined (e.g., $\underline{r}$).

Figure 11: A vector displacement

The vector displacement ${\bf r}$ can also be specified in terms of its coordinates:

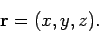$${\bf r} = (x, y, z).$$ (30)

The above expression is interpreted as follows: in order to get from point $O$ to point $R$, first move $x$ meters along the $x$-axis (perpendicular to both the $y$- and $z$-axes), then move $y$ meters along the $y$-axis (perpendicular to both the $x$- and $z$-axes), finally move $z$ meters along the $z$-axis (perpendicular to both the $x$- and $y$-axes). Note that a positive $x$ value is interpreted as an instruction to move $x$ meters along the $x$-axis in the direction of increasing $x$, whereas a negative $x$ value is interpreted as an instruction to move $\vert x\vert$ meters along the $x$-axis in the opposite direction, and so on.