


Next: Worked example 12.5: Mass
Up: Orbital motion
Previous: Worked example 12.3: Circular
Question: The distance of closest approach of Halley's comet to the
Sun is
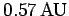 . (1 AU is the mean Earth-Sun distance.) The greatest
distance of the comet from the Sun is 35AU. The comet's speed at closest approach
is
. (1 AU is the mean Earth-Sun distance.) The greatest
distance of the comet from the Sun is 35AU. The comet's speed at closest approach
is
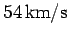 . What is its speed when it is furthest from the Sun?
. What is its speed when it is furthest from the Sun?
Answer: At perihelion and aphelion, the comet's velocity is
perpendicular to its position vector from the Sun. Hence, at these two
special points, the comet's angular momentum (around the Sun) takes the particularly
simple form
Here,  is the comet's mass,
is the comet's mass,  is its distance from the Sun, and
is its distance from the Sun, and  is its speed.
According to Kepler's second law, the comet orbits the Sun with constant angular
momentum. Hence, we can write
is its speed.
According to Kepler's second law, the comet orbits the Sun with constant angular
momentum. Hence, we can write
where 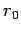 and
and 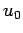 are the perihelion distance and speed, respectively, and
are the perihelion distance and speed, respectively, and 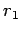 and
and 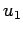 are the corresponding quantities at aphelion. We are told that
are the corresponding quantities at aphelion. We are told that
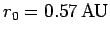 ,
,
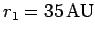 ,
and
,
and
 . It follows that
. It follows that



Next: Worked example 12.5: Mass
Up: Orbital motion
Previous: Worked example 12.3: Circular
Richard Fitzpatrick
2006-02-02