


Next: Worked example 12.1: Gravity
Up: Orbital motion
Previous: Satellite orbits
Let us now see whether we can use Newton's universal laws of motion to derive
Kepler's laws of planetary motion. Consider a planet orbiting around the Sun.
It is convenient to specify the planet's instantaneous position,
with respect to the Sun, in terms of the polar coordinates  and
and  .
As illustrated in Fig. 105,
.
As illustrated in Fig. 105,  is the radial distance between the planet and the
Sun, whereas
is the radial distance between the planet and the
Sun, whereas  is the angular bearing of the planet, from the Sun,
measured with respect to some arbitrarily chosen direction.
is the angular bearing of the planet, from the Sun,
measured with respect to some arbitrarily chosen direction.
Figure 105:
A planetary orbit.
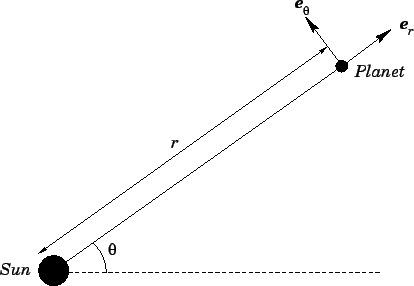 |
Let us define two unit vectors,  and
and
 . (A unit vector is
simply a vector whose length is unity.) As shown in Fig. 105, the radial
unit vector
. (A unit vector is
simply a vector whose length is unity.) As shown in Fig. 105, the radial
unit vector  always points from the Sun towards the instantaneous position
of the planet. Moreover, the tangential unit vector
always points from the Sun towards the instantaneous position
of the planet. Moreover, the tangential unit vector
 is always
normal to
is always
normal to  , in the direction of increasing
, in the direction of increasing  .
In Sect. 7.5, we demonstrated that when acceleration is written in terms of polar
coordinates, it takes the form
.
In Sect. 7.5, we demonstrated that when acceleration is written in terms of polar
coordinates, it takes the form
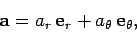 |
(562) |
where
These expressions are more complicated that the corresponding cartesian expressions
because the unit vectors  and
and
 change direction
as the planet changes position.
change direction
as the planet changes position.
Now, the planet is subject to a single force: i.e., the force of gravitational attraction exerted
by the Sun. In polar coordinates, this force takes a particularly simple
form (which is why we are using polar coordinates):
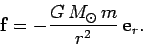 |
(565) |
The minus sign indicates that the force is directed towards, rather than away from, the Sun.
According to Newton's second law, the planet's equation of motion is written
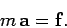 |
(566) |
The above four equations yield
Equation (568) reduces to
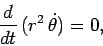 |
(569) |
or
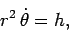 |
(570) |
where 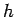 is a constant of the motion. What is the physical interpretation of
is a constant of the motion. What is the physical interpretation of 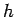 ? Recall,
from Sect. 9.2, that the angular momentum vector of a point particle can be written
? Recall,
from Sect. 9.2, that the angular momentum vector of a point particle can be written
 |
(571) |
For the case in hand,
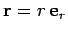 and
and
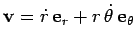 [see Sect. 7.5]. Hence,
[see Sect. 7.5]. Hence,
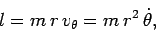 |
(572) |
yielding
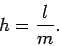 |
(573) |
Clearly, 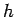 represents the angular momentum (per unit mass) of our planet around the Sun.
Angular momentum is conserved (i.e.,
represents the angular momentum (per unit mass) of our planet around the Sun.
Angular momentum is conserved (i.e., 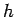 is constant)
because the force of gravitational attraction between the planet and
the Sun exerts zero torque on the planet. (Recall, from Sect. 9, that torque is the
rate of change of angular momentum.)
The torque is zero because the gravitational force is radial in nature: i.e.,
its line of action passes through the Sun, and so its associated lever arm is of length zero.
is constant)
because the force of gravitational attraction between the planet and
the Sun exerts zero torque on the planet. (Recall, from Sect. 9, that torque is the
rate of change of angular momentum.)
The torque is zero because the gravitational force is radial in nature: i.e.,
its line of action passes through the Sun, and so its associated lever arm is of length zero.
Figure 106:
The origin of Kepler's second law.
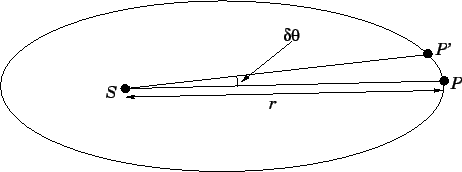 |
The quantity 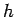 has another physical interpretation. Consider Fig. 106. Suppose that
our planet moves from
has another physical interpretation. Consider Fig. 106. Suppose that
our planet moves from 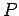 to
to 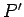 in the short time interval
in the short time interval  . Here,
. Here, 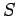 represents
the position of the Sun. The lines
represents
the position of the Sun. The lines 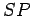 and
and 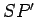 are both approximately of length
are both approximately of length  .
Moreover, using simple trigonometry, the line
.
Moreover, using simple trigonometry, the line 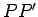 is of length
is of length
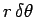 , where
, where
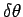 is the small angle through which the line joining the Sun and the planet
rotates in the time interval
is the small angle through which the line joining the Sun and the planet
rotates in the time interval  . The area of the triangle
. The area of the triangle 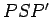 is approximately
is approximately
 |
(574) |
i.e., half its base times its height. Of course, this area represents the area swept out
by the line joining the Sun and the planet in the time interval  . Hence, the
rate at which this area is swept is given by
. Hence, the
rate at which this area is swept is given by
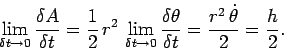 |
(575) |
Clearly, the fact that 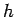 is a constant of the motion implies that the line joining the planet and
the Sun sweeps out area at a constant rate: i.e., the line sweeps equal areas in equal time intervals.
But, this is just Kepler's second law. We conclude that Kepler's second law of planetary motion is a direct manifestation of
angular momentum conservation.
is a constant of the motion implies that the line joining the planet and
the Sun sweeps out area at a constant rate: i.e., the line sweeps equal areas in equal time intervals.
But, this is just Kepler's second law. We conclude that Kepler's second law of planetary motion is a direct manifestation of
angular momentum conservation.
Let
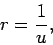 |
(576) |
where
 is a new radial variable. Differentiating with respect to
is a new radial variable. Differentiating with respect to  , we obtain
, we obtain
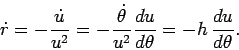 |
(577) |
The last step follows from the fact that
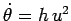 . Differentiating a second time
with respect to
. Differentiating a second time
with respect to  , we obtain
, we obtain
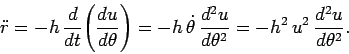 |
(578) |
Equations (567) and (578) can be combined to give
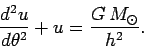 |
(579) |
This equation possesses the fairly obvious general solution
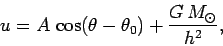 |
(580) |
where  and
and 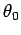 are arbitrary constants.
are arbitrary constants.
The above formula can be inverted to give the following simple orbit equation for our planet:
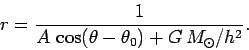 |
(581) |
The constant 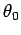 merely determines the orientation of the orbit. Since we are
only interested in the orbit's shape, we can set this quantity to zero without
loss of generality. Hence, our orbit equation reduces to
merely determines the orientation of the orbit. Since we are
only interested in the orbit's shape, we can set this quantity to zero without
loss of generality. Hence, our orbit equation reduces to
 |
(582) |
where
 |
(583) |
and
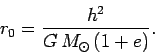 |
(584) |
Formula (582) is the standard equation of an ellipse (assuming  ), with the
origin at a focus. Hence, we have now proved Kepler's first law of planetary motion.
It is clear that
), with the
origin at a focus. Hence, we have now proved Kepler's first law of planetary motion.
It is clear that 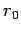 is the radial distance at
is the radial distance at 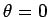 . The radial distance at
. The radial distance at
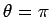 is written
is written
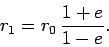 |
(585) |
Here, 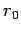 is termed the perihelion distance (i.e., the closest distance to the
Sun) and
is termed the perihelion distance (i.e., the closest distance to the
Sun) and 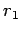 is termed the aphelion distance (i.e., the furthest distance from the
Sun). The quantity
is termed the aphelion distance (i.e., the furthest distance from the
Sun). The quantity
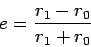 |
(586) |
is termed the eccentricity of the orbit, and is a measure of its departure from
circularity. Thus,  corresponds to a purely circular orbit, whereas
corresponds to a purely circular orbit, whereas
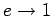 corresponds to a highly elongated orbit. As specified in Tab. 7, the orbital
eccentricities of all of the planets (except Mercury) are fairly small.
corresponds to a highly elongated orbit. As specified in Tab. 7, the orbital
eccentricities of all of the planets (except Mercury) are fairly small.
Table 7:
The orbital eccentricities of various planets in the Solar System.
| Planet |
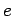 |
| Mercury |
0.206 |
| Venus |
0.007 |
| Earth |
0.017 |
| Mars |
0.093 |
| Jupiter |
0.048 |
| Saturn |
0.056 |
|
According to Eq. (575), a line joining the Sun and an orbiting planet sweeps area
at the constant rate  . Let
. Let 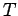 be the planet's orbital period. We expect the line to
sweep out the whole area of the ellipse enclosed by the planet's orbit in the time
interval
be the planet's orbital period. We expect the line to
sweep out the whole area of the ellipse enclosed by the planet's orbit in the time
interval 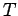 . Since the area of an ellipse is
. Since the area of an ellipse is 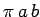 , where
, where  and
and 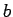 are the
semi-major and semi-minor axes, we can write
are the
semi-major and semi-minor axes, we can write
 |
(587) |
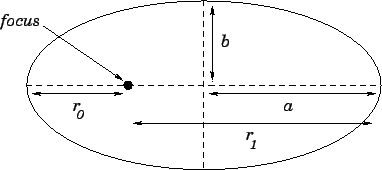
Incidentally, Fig. 107 illustrates the relationship between the aphelion distance, the
perihelion distance, and the semi-major and semi-minor axes of a planetary orbit. It is
clear, from the figure, that the semi-major axis is just the mean of the aphelion and
perihelion distances: i.e.,
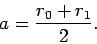 |
(588) |
Thus,  is essentially the planet's mean distance from the Sun. Finally, the relationship between
is essentially the planet's mean distance from the Sun. Finally, the relationship between  ,
, 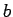 ,
and the eccentricity,
,
and the eccentricity, 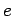 , is given by the well-known formula
, is given by the well-known formula
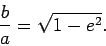 |
(589) |
This formula can easily be obtained from Eq. (582).
Figure 107:
Anatomy of a planetary orbit.
 |
Equations (584), (585), and (588) can be combined to give
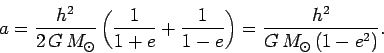 |
(590) |
It follows, from Eqs. (587), (589), and (590), that the orbital period
can be written
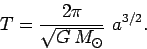 |
(591) |
Thus, the orbital period of a planet is proportional to its mean distance from the Sun to
the power 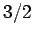 --the constant of proportionality being the same for all planets. Of course,
this is just Kepler's third law of planetary motion.
--the constant of proportionality being the same for all planets. Of course,
this is just Kepler's third law of planetary motion.



Next: Worked example 12.1: Gravity
Up: Orbital motion
Previous: Satellite orbits
Richard Fitzpatrick
2006-02-02

![]() and
and
![]() . (A unit vector is
simply a vector whose length is unity.) As shown in Fig. 105, the radial
unit vector
. (A unit vector is
simply a vector whose length is unity.) As shown in Fig. 105, the radial
unit vector ![]() always points from the Sun towards the instantaneous position
of the planet. Moreover, the tangential unit vector
always points from the Sun towards the instantaneous position
of the planet. Moreover, the tangential unit vector
![]() is always
normal to
is always
normal to ![]() , in the direction of increasing
, in the direction of increasing ![]() .
In Sect. 7.5, we demonstrated that when acceleration is written in terms of polar
coordinates, it takes the form
.
In Sect. 7.5, we demonstrated that when acceleration is written in terms of polar
coordinates, it takes the form
![]() has another physical interpretation. Consider Fig. 106. Suppose that
our planet moves from
has another physical interpretation. Consider Fig. 106. Suppose that
our planet moves from ![]() to
to ![]() in the short time interval
in the short time interval ![]() . Here,
. Here, ![]() represents
the position of the Sun. The lines
represents
the position of the Sun. The lines ![]() and
and ![]() are both approximately of length
are both approximately of length ![]() .
Moreover, using simple trigonometry, the line
.
Moreover, using simple trigonometry, the line ![]() is of length
is of length
![]() , where
, where
![]() is the small angle through which the line joining the Sun and the planet
rotates in the time interval
is the small angle through which the line joining the Sun and the planet
rotates in the time interval ![]() . The area of the triangle
. The area of the triangle ![]() is approximately
is approximately
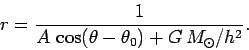

![]() ), with the
origin at a focus. Hence, we have now proved Kepler's first law of planetary motion.
It is clear that
), with the
origin at a focus. Hence, we have now proved Kepler's first law of planetary motion.
It is clear that ![]() is the radial distance at
is the radial distance at ![]() . The radial distance at
. The radial distance at
![]() is written
is written
![]() . Let
. Let ![]() be the planet's orbital period. We expect the line to
sweep out the whole area of the ellipse enclosed by the planet's orbit in the time
interval
be the planet's orbital period. We expect the line to
sweep out the whole area of the ellipse enclosed by the planet's orbit in the time
interval ![]() . Since the area of an ellipse is
. Since the area of an ellipse is ![]() , where
, where ![]() and
and ![]() are the
semi-major and semi-minor axes, we can write
are the
semi-major and semi-minor axes, we can write