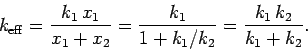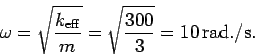Next: Worked example 11.4: Energy
Up: Oscillatory motion
Previous: Worked example 11.2: Block
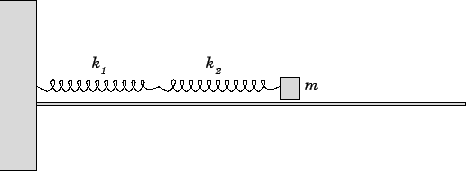
Question: A block of mass  is attached to
two springs, as shown below, and slides over a horizontal frictionless
surface. Given that the force constants of the two springs
are
is attached to
two springs, as shown below, and slides over a horizontal frictionless
surface. Given that the force constants of the two springs
are
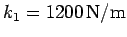 and
and
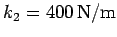 , find the period
of oscillation of the system.
, find the period
of oscillation of the system.
Answer:
Let 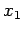 and
and  represent the extensions of the first and second springs, respectively.
The net displacement
represent the extensions of the first and second springs, respectively.
The net displacement  of the mass from its equilibrium position is then given by
of the mass from its equilibrium position is then given by
Let
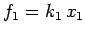 and
and 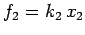 be the magnitudes of the forces exerted by the first and second springs,
respectively. Since the springs (presumably) possess negligible inertia,
they must exert equal and opposite forces on one another. This implies that
be the magnitudes of the forces exerted by the first and second springs,
respectively. Since the springs (presumably) possess negligible inertia,
they must exert equal and opposite forces on one another. This implies that 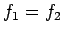 , or
, or
Finally, if 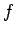 is the magnitude of the restoring force acting on the mass, then
force balance implies that
is the magnitude of the restoring force acting on the mass, then
force balance implies that 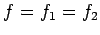 , or
, or
Here,  is the effective force constant of the two springs.
The above equations can be combined to give
is the effective force constant of the two springs.
The above equations can be combined to give
Thus, the problem reduces to that of a block of mass  attached to
a spring of effective force constant
attached to
a spring of effective force constant
The angular frequency of oscillation is immediately given by the standard formula
Hence, the period of oscillation is



Next: Worked example 11.4: Energy
Up: Oscillatory motion
Previous: Worked example 11.2: Block
Richard Fitzpatrick
2006-02-02

![]() and
and ![]() represent the extensions of the first and second springs, respectively.
The net displacement
represent the extensions of the first and second springs, respectively.
The net displacement ![]() of the mass from its equilibrium position is then given by
of the mass from its equilibrium position is then given by